![]()
Review pages 76-84 (Section 2.3 and 2.4)
Stack
StackEmptyException
Queue
QueueEmptyException
ArrayStack
StackFullException
ArrayQueue
QueueFullException
Review pages 159-163 (Section 4.3.1)
![]()
Deque
DequeEmptyException
DLNode
LinkedDeque
DequeStack
InspectableContainer
InspectableVector
Vector
/** Reverses a linked list. @param node First node of the linked list to be reversed. @return First node of the reversed list. */ public static Node reverse(Node node)
![]()
Review pages 111-118 (Section 3.5 and 3.6.1)
Position
InspectablePositionalContainer
PositionalContainer
InspectableList
EmptyContainerException
List
DNode
NodeList
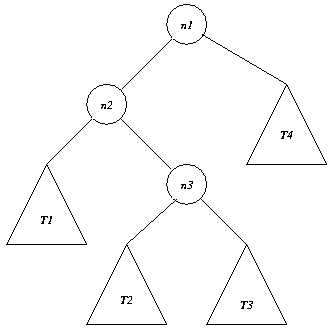
List whose elements are one of the following objects
public static final Object RED = new Object(); public static final Object WHITE = new Object(); public static final Object BLUE = new Object();The list may contain each object more than once. Write a method
public static void sort(List list)that sorts the elements: first all the red, then the white and finally the blue objects.
A loop invariant is also a predicate. It tells us something about the
values of the variables while executing a loop. This predicate should be
satisfied at the beginning of every iteration of the loop. Consider the
loop
while B do S
with loop invariant LI. If
{ LI  B }
S { LI },
B }
S { LI },
that is, statement S preserves the loop invariant LI
within the loop, then we can conclude that
{ LI } while B do S
{ LI 
 B },
B },
that is, if the loop invariant LI is satisfied at
the start of the execution of the loop and the loop terminates then the
loop invariant LI (and of course also
 B) is satisfied at termination.
B) is satisfied at termination.
Consider the following Java snippet.
int i = 1;
int x = 1;
while (i < N)
{
x *= i + 1;
i++;
}
For the above loop, the assertion x = i!  i <= N is a
loop invariant.
i <= N is a
loop invariant.
Algorithm bubbleSort(sequence):
Input: sequence of integers sequence
Postcondition: sequence is sorted and
contains the same integers as the original sequence
length  length of sequence
length of sequence
i  0
0
while i < length do
j  0
0
while j < length - 1 do
if jth element of sequence > (j+1)th element of
sequence then
swap jth and (j+1)th element of sequence
The outer loop has loop invariant
(A k : length - i <= k < length :
(A l : k < l < length :
kth element of sequence <= lth element of sequence))
and the inner loop has loop invariant
(A k : length - i <= k < length :
(A l : k < l < length :
kth element of sequence <= lth element of sequence)) 
(A k : 0 <= k < j :
kth element of sequence <= jth element of sequence)
![]()
Algorithm isBST(t):
Input: binary tree whose nodes contains integers
Output: Is t a binary search tree?
![]()
InspectableBinaryTree
BinaryTree
Algorithm isBST(t):
Input: binary tree whose nodes contains integers
Output: Is t a binary search tree?
if t consists of a single node then
result  true
true
else
result  isBST(left subtree of t)
isBST(left subtree of t)
 isBST(right subtree of t)
isBST(right subtree of t)
 smallerOrEqual(left subtree of t, integer of root of t)
smallerOrEqual(left subtree of t, integer of root of t)
 greaterOrEqual(right subtree of t, integer of root of t)
greaterOrEqual(right subtree of t, integer of root of t)
return result
Algorithm smallerOrEqual(t, i):
Input: binary tree whose nodes contains integers; an integer
Output: (A n : n is a node of t : element of n <= i)
result  element of root of t <= i
element of root of t <= i
if t consists of more than one node then
result  result
result
 smallerOrEqual(left subtree of t, i)
smallerOrEqual(left subtree of t, i)
 smallerOrEqual(right subtree of t, i)
smallerOrEqual(right subtree of t, i)
return result
Algorithm greaterOrEqual(t, i):
Input: binary tree whose nodes contains integers; an integer
Output: (A n : n is a node of t : element of n >=
i)
result  element of root of t >= i
element of root of t >= i
if t consists of more than one node then
result  result
result
 greaterOrEqual(left subtree of t, i)
greaterOrEqual(left subtree of t, i)
 greaterOrEqual(right subtree of t, i)
greaterOrEqual(right subtree of t, i)
return result
![]()
![]()
![]()
Dictionary d = new ...();
d.insertItem(new Integer(2), new Object());
if (d.findElement(new Integer(3)) == Dictionary.NO_SUCH_KEY))
{
System.out.println("Not found!");
}
else
{
System.out.println("Found!");
}
Explain why we cannot use
Dictionary.NO_SUCH_KEY.equals(d.findElement(new Integer(3)))
instead of
d.findElement(new Integer(3)) == Dictionary.NO_SUCH_KEY).
![]()
"More output"
Algorithm isBST(tree):
Input: a binary tree whose nodes contains keys
Output: (Is tree a binary search tree?,
minimal key stored in tree, maximal key stored in tree)
if tree has one node then
result  (true, key of root of tree, key of root of tree)
(true, key of root of tree, key of root of tree)
else
(isBSTleft, minleft, maxleft)
 isBST(left subtree of tree)
isBST(left subtree of tree)
(isBSTright, minright, maxright)
 isBST(right subtree of tree)
isBST(right subtree of tree)
isBST  isBSTleft
isBSTleft  isBSTright
isBSTright  maxleft <= key of root of tree <= minright
maxleft <= key of root of tree <= minright
min  min(key of root of tree, minleft, minright)
min(key of root of tree, minleft, minright)
max  min(key of root of tree, maxleft, maxright)
min(key of root of tree, maxleft, maxright)
result  (isBST, min, max)
(isBST, min, max)
return result
"More input"
Algorithm isBST(tree, min, max):
Input: a binary tree whose nodes contains keys; key; key
Output: Is tree a binary search tree?  (A node : node is a node of tree : min <= key of node <= max)
(A node : node is a node of tree : min <= key of node <= max)
if tree has one node then
result  min <= key of root of tree <= max
min <= key of root of tree <= max
else
result  min <= key of root of tree <= max
min <= key of root of tree <= max  isBST(left subtree of tree, min, min(key of root of tree, max))
isBST(left subtree of tree, min, min(key of root of tree, max))  isBST(right subtree of tree, max(min, key of root of tree), max)
isBST(right subtree of tree, max(min, key of root of tree), max)
return result
Implementation of a binary tree by means of an array
Algorithm removeAboveExternal(node):
Precondition: node is external and different from the root
Input: a node of the binary tree
Postcondition: node and its parent have been removed from the tree
and the sibling of node takes the place of its parent
Output: the element of the parent of node
index  index of node
index of node
parent  index div 2
index div 2
element  element of tree[parent]
element of tree[parent]
sibling  index + 1 - 2 * (index mod 2)
index + 1 - 2 * (index mod 2)
move(sibling, parent)
size  size - 2
size - 2
return element
Algorithm move(old, new):
Precondition: old is the index of a child of the node with index new
Input: two indices of nodes
Postcondition: the subtree rooted at node with index old replaces the subtree rooted at node with index new
tree[new]  tree[old]
tree[old]
if tree[old] is an internal node then
move(2 * old, 2 * new)
move(2 * old + 1, 2 * new + 1)
else
tree[2 * new]  empty
empty
tree[2 * new + 1]  empty
empty
![]()
![]()
Algorithm removeAll(key):
Input: key
Output: collection of elements of items in tree whose key is key
Postcondition: items whose key is key have been
removed from tree
collection  empty collection
empty collection
removeAll(key, root of tree, collection)
return collection
Algorithm removeAll(key, node, collection):
Input: key; node of tree; collection of elements
Postcondition: elements of items in subtree rooted at node whose key is key have been added to collection and those items have been removed from subtree rooted at node
if node is not a leaf then
if key of node > key then
removeAll(key, left child of node, collection)
else if key of node < key then
removeAll(key, right child of node, collection)
else
removeAll(key, right child of node, collection)
element  remove(key, node)
remove(key, node)
add element to collection
![]()
![]()
Implementation of a priority queue by means of an (un)sorted sequence in PostScript and PDF.
![]()
Proof of Proposition 7.5 in PostScript and PDF
Assume we have the following heap.
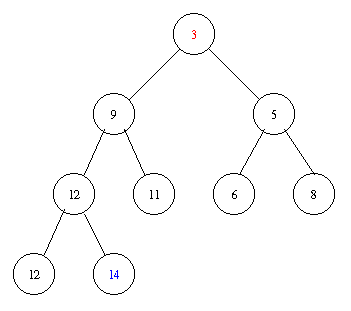
Removing the minimal element takes the following steps.
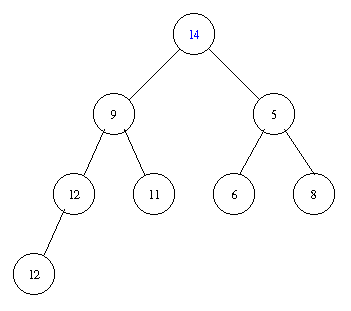
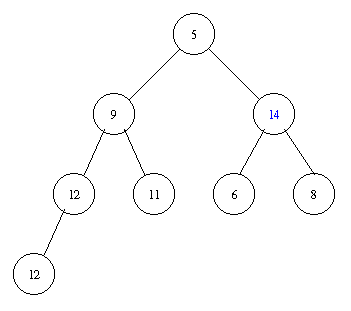
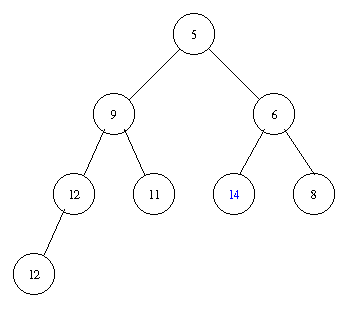
Inserting an element with key 8 takes the following steps.
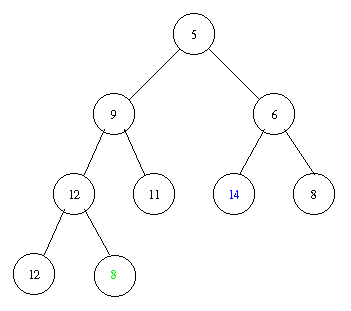
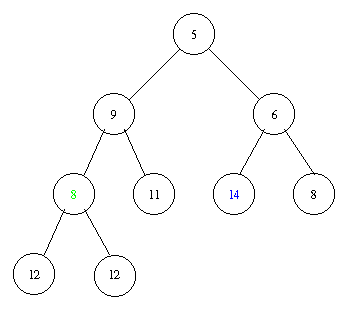
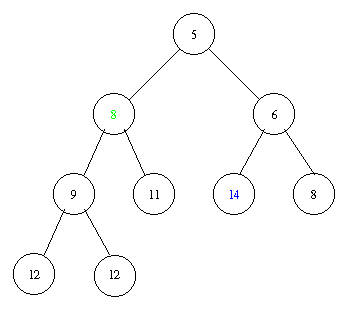
Implementation of a priority queue with a heap in pseudocode: PostScript and PDF
/**
Returns the minimum of the specified matrix.
The specified matrix is assumed to have the same number of rows as columns.
@param matrix a two-dimensional array of integers.
@return the minimum of the specified matrix.
*/
public static Integer minimum(Integer[][] matrix)
{
final int DIMENSION = matrix.length;
PriorityQueue minQueue = new ?PriorityQueue(new IntegerComparator());
for (int r = 0; r < DIMENSION; r++)
{
PriorityQueue rowQueue = new ?PriorityQueue(new IntegerComparator());
for (int c = 0; c < DIMENSION; c++)
{
rowQueue.insertItem(new Item(matrix[r][c], matrix[r][c]));
}
Object element = rowQueue.removeMin();
minQueue.insertItem(new Item(element, element));
}
return minQueue.removeMin();
}
The priority queues minQueue and rowQueue can be implemented
either by a sorted sequence, an unsorted sequence or a heap. Which choice
for these priority queues gives rise to the most efficient algorithm
(the algorithm with the best worst case running time)? What is the worst
case running time for those choices?
![]()
LongHashCode
PolynomialHashCode
CyclicShiftHashCode

Implementation of a simple graph by means of an adjacency list: PostScript and PDF
In the implementation of a graph by means of an adjacency matrix, we restrict our attention to undirected graphs. There are simple mixed graphs whose representation by means of an adjacency matrix give rise to a matrix in which cells contain more than one edge (Can you think of an example?).