5 Differential drive robot
The robot you are using in this lab is called a differential drive robot. A differential drive robot has two independently driven wheels mounted on a common axis. The motion of a differential drive robot can be controlled by controlling the velocities of the two wheels. The robot moves:
- in a straight line if both wheels turn in the same direction at the same speed
- spins in place if the wheels turn in oppposite directions at the same speed
- turning left if the both wheels turn in the same direction and the left wheel turns slower than the right wheel
- turning right if the both wheels turn in the same direction and the right wheel turns slower than the left wheel
A picture of the robot is shown below; note that the front of the robot is the side where the two wheels are mounted.

5.1 Kinematics of a differential drive robot
Mechanics is the study of motion of (macroscopic) objects. Kinematics is the part of mechanics that describes the motion of objects without considering the forces that cause the motion.
The kinematics of a differential drive robot are given by the velocities of its two wheels. By controlling the wheel velocities, we can control the motion of a differential drive.
Consider a differential drive robot where the distance between the wheels is \(L\), the right wheel ground velocity is \(v_r\), and the left wheel ground velocity is \(v_l\). The path of the robot is a circular arc of radius \(R\) as shown in the figure below:
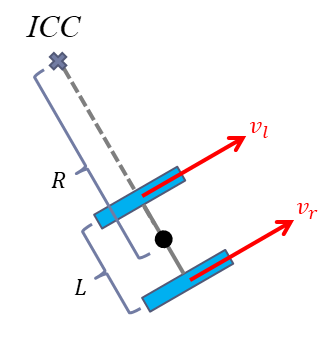
The point labelled \(ICC\) is called the instantaneous center of curvature. It can be shown that the radius of the circle that the robot is travelling on is given by:
\[ R = \frac{L(v_l + v_r)}{2 (v_r - v_l)} \]
and that the angular velocity about the \(ICC\) is given by:
\[ \omega = \frac{v_r - v_l}{L} \]
The motion of the robot has four interesting cases:
- if \(v_l = v_r\) then \(\omega = 0\) and \(R \rightarrow \infty\); the robot moves in a straight line
- if \(v_l = 0\) and \(v_r \neq 0\) then \(R = L / 2\); the robot spins on its left wheel with the direction of the spinning determined by the sign of the velocity of the right wheel
- if \(v_r = 0\) and \(v_l \neq 0\) then \(R = -L / 2\); the robot spins on its right wheel with the direction of the spinning determined by the sign of the velocity of the left wheel
- if \(v_l = -v_r\) then \(R = 0\); the robot spins in place about the midpoint of the wheel axis with the direction of the spinning determined by the signs of the wheel velocities
In all other cases both wheels move and the robot travels in a circular arc.