5 The Rayleigh density function
The Rayleigh distribution occurs when you compute the magnitudes of multiple noisy vectors. The figure below shows five instances of the Rayleigh distribution for different values of the scale parameter \(\sigma\):
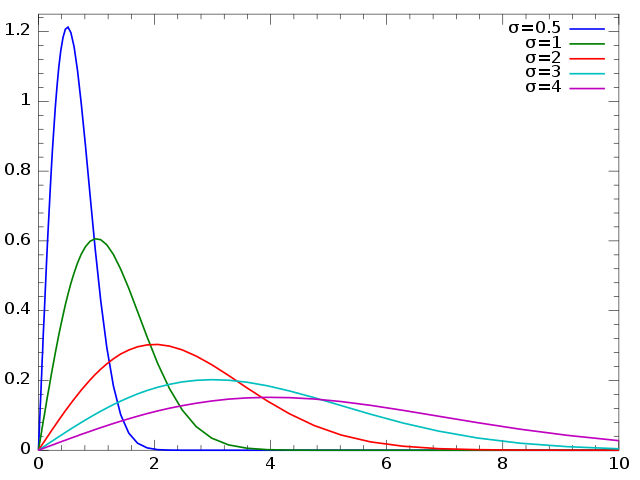
Figure 5.1: Five Rayleigh density functions having different scale parameters \(\sigma\).
The equation of the Rayleigh density function shown in the figure above is given by:
\[y = \frac{x}{\sigma^2} e^{-x^2/(2\sigma^2)}\]
In MATLAB open the file named rayleighpdf.m. This file contains a function that when completed returns the value of the function shown above.
Complete the function so that it returns the value y as defined by the equation above.
The MATLAB function exp can be used to compute the value of \(e^x\). Review the help documentation for the method to determine how to use it correctly.
5.1 Using rayleighpdf.m
Test your function by typing the following in the MATLAB Command Window:
x = 4;
sigma = 2;
pdf = rayleighpdf(x, sigma)A correct function would cause the value 0.1353 to be output. If the correct value is not output, review your function and correct any errors that you find.
For values of \(x\) that are far away from the peak of the distribution, the function should return a value that is approximately equal to zero; for example, if we have a Rayleigh density function with \(\sigma = 1\) then evaluating the function at \(x = 10\) should produce a value of zero:
y = rayleighpdf(10, 1)5.2 Solve a simple problem using rayleighpdf.m
What value of \(x\) produces a value of the Rayleigh probability density function of \(y = 0.2\) if \(\sigma = 2\)? Note that there are two possible values for \(x\) but we are interested in the larger of the two values.
In MATLAB, open the script file solveForX.m. Complete the script so that it does the following:
- creates a variable named
xthat when passed to yourrayleighpdffunction causesrayleighpdfto return a value that is very close to \(0.2\). Your value ofxmust be within \(0.1\) of the - creates a varialbe named
pdfthat stores the value returned byrayleighpdfwhen you call it with your value forx(andsigmaequal to 2).
You should find an appropriate value of x by using trial and error; referring to the figure above will help you to quickly find an appropriate value of x.
Your script must use the function rayleighpdf that you created earlier.