6 Point on a spiral
The coordinates \((x, y)\) of a point on a logarithmic spiral are given by:
\[ \begin{eqnarray*} r & = & a e^{b \theta}\\ x & = & r \cos (\theta)\\ y & = & r \sin (\theta)\\ \end{eqnarray*} \]
where \(\theta\) is the angle measured from the positive \(x\)-axis. The figure below shows a logarithmic spiral having parameters \(a = 1\) and \(b = 0.2\) drawn over \(0 \leq \theta \leq 4 \pi\).
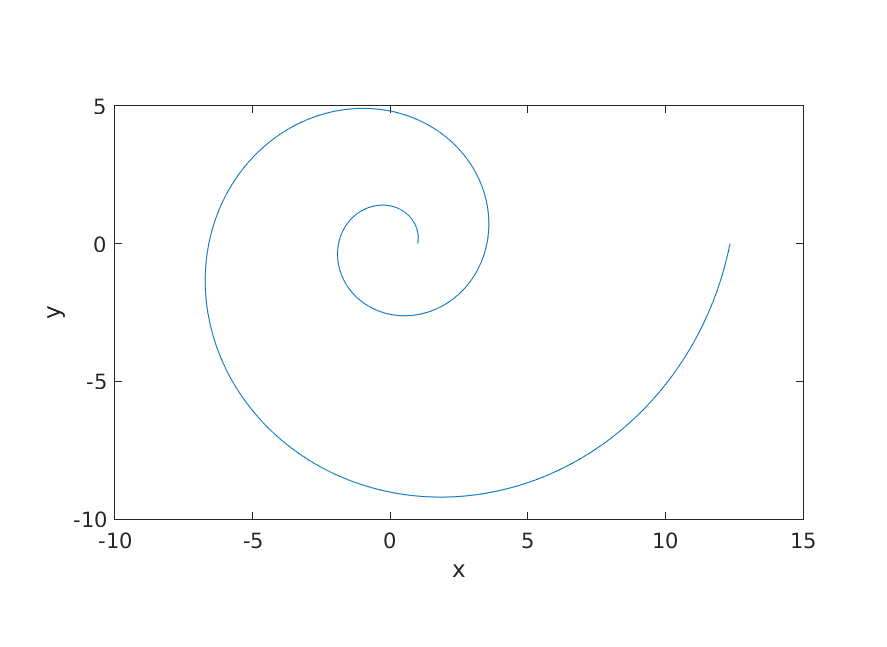
Figure 6.1: A logarithmic spiral.
In MATLAB, open the file pointOnLogSpiral.m. This file contains a user-defined function that when completed returns the coordinates of the point \((x, y)\) located at an angle of \(\theta\) on a logarithmic spiral having parameters a and b.
Complete the function remembering to save the file every time that you edit it.
6.1 Using pointOnLogSpiral.m
Test your function by typing the following in the MATLAB Command Window:
ang = 0;
a = 1.5;
b = 0.1;
[x, y] = pointOnLogSpiral(ang, a, b)A correct function would cause the following to be output:
x =
1.5000
y =
0If the correct value is not output, review your function and correct any errors that you find.
6.2 Plot a circle using pointOnLogSpiral.m
We can generate multiple points on a circle with the following MATLAB code:
% 100 evenly spaced values between 0 and 4pi
theta = linspace(0, 4 * pi, 100);
% 100 ones
a = ones(1, 100);
% 100 0.2s
b = 0.2 * ones(1, 100);
% call pointOnLogSpiral using the 100 sets of values
[x, y] = arrayfun(@pointOnLogSpiral, theta, a, b);We can plot the points defined by the vectors x and y to produce the following figure:
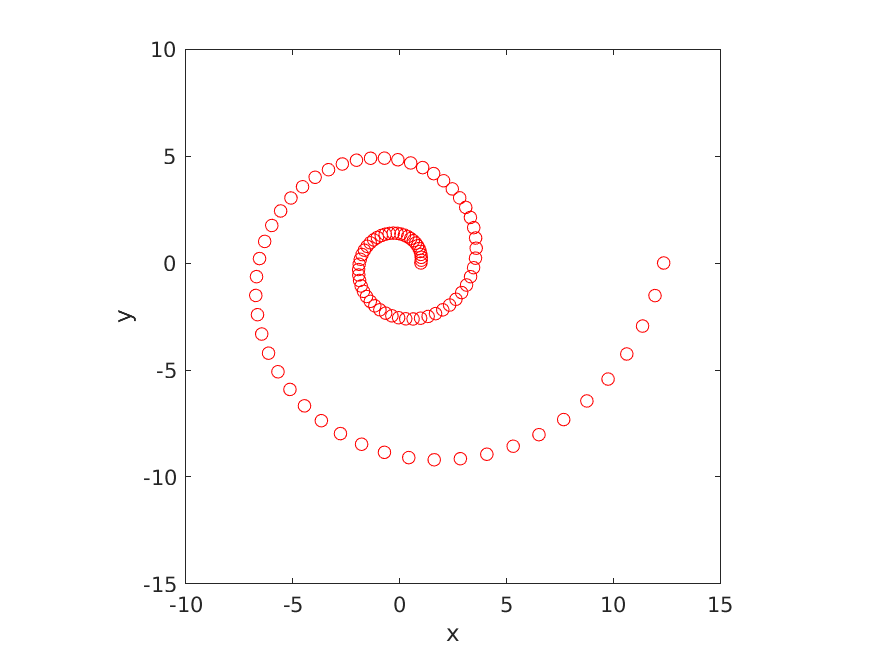
Figure 6.2: Three normal probability density functions having different mean values.
In MATLAB, open the file plotSpiral.m. This file contains a script that when completed should generate the identical figure to that shown above.
To produce the circle shown above, we use the following steps:
- plot the points in
xandyusing red circles - set the aspect ratio of the axes so that equal tick mark increments on the x- and y-axis are equal in size
- set the limits of the x and y axes
- label the x-axis
- label the y-axis
Each one of the five steps shown above is accomplished using a different MATLAB function (Steps 2 and 3 are accomplished using the same function but using different input values for the function). The functions that you need to use in the order that you need to use them are:
plotaxisaxisxlabelylabel
Read the documentation for each function to determine how to use the function to accomplish each of the five steps required to generate the plot. You can use the help facility in MATLAB to easily determine how to accomplish each of the five steps:
help plothelp axishelp xlabelhelp ylabelComplete the script plotCircle.m and run the script to verify that it produces a plot identical to the one shown above.
More detailed information on each of the functions can be found uisng the links to the documentation below; note that there might be too much information for beginners to easily digest if you use the online documentation: