Birthday Paradox

In a room of people, at what number $n$ of people in the room is there a 50-50 chance of at least two people having the same birthday?

For simplicity, we will assume the year has 365 days. Once we calculate the number, the answer will be somewhat counter-intuitive, but it's only a “paradox” because our brains don't fully understand the compounding power of exponents.

We use Python to help with the calculations that solve the problem and to display the results graphically. We will also review some simple probability theory to help us formulate the problem in way that facilitates its solution.

Follow along this tutorial by logging in to https://pythoncode.eecs.yorku.ca and select the "Tutorial Mode" (enable pop=ups when requested to see the plots).

Probability

Example

Here’s an example: What’s the chance of getting 10 heads in a row when flipping fair coin2?¹

One might be tempted to think as follows: Well, getting one head is a $50\%$ chance. Getting two heads is twice as hard, so a 25% chance. Getting ten heads is probably 10 times harder, so about $50\%/10$ or a 5% chance.

That answer would be incorrect.

Suppose we have a fair coin which we toss three times in row. The sample space of 8 outcomes is the set:

$$\{HHH, HHT, HTH, HTT, THH, THT, TTH, TTT\}$$

Each of those outcomes has $1/8$ probability of occurring. Thus the probability of event HHH (three heads in a row) is not $(0.5)/3 \approx 0.1667$. Rather it is:

$$P(\{HHH\}) = 1/8 = 0.5 \cdot 0.5 \cdot 0.5 = 0.5^{3} = 0.125$$

Brief review of simple probability

Truth and falsity are the subject of logic. There are some things we believe to be true and others false. But there are many things that are uncertain, i.e. their truth and falsity are not known to us, and we can be uncertain to varying degrees. From our intuitions about uncertainty, a calculus has been developed over the last 150 years to help us reason about uncertainty, in the same way that a calculus of logic helps us reason about validity. [The online Merriam Webster dictionary defines "reason" as "the power of comprehending, inferring, or thinking especially in orderly rational ways".]

A sample space is a set of possible outcomes of a random process. An event is is a subset of the sample space. If $S$ is a finite sample space in which all all outcomes are equally likely, then the probability of event E (denoted $P(E))$) is

$$P(E) = \frac{\mbox{number of outcomes in }E}{\mbox{total number of outcomes in }S} = \frac{card(E)}{card(S)}$$

Formally, $P$ is a probability function from the set of all events in $S$ to the set of real numbers satisfying the following three axioms. For all events $A$ and $B$ in $S$:

1. $0 \leq P(A) \leq 1$
2. $P(\emptyset) = 0$ and $P(S) = 1$.
3. If $A$ and $B$ are disjoint sets (i.e. $A \cap B = \emptyset$), then $P(A \cup B) = P(A) + P(B)$.

The following theorem can be deduced from the axioms. For any events $A$ and $B$ (disjoint or not):

$$P(A \cup B) = P(A) + P(B) + P(A \cap B)$$

Let $E_1$ be the event that the first toss is heads (i.e. subset $\{HHH, HHT, HTH, HTT\}$), and let $E_2$ be the event that the second toss is heads (i.e. subset $\{HHH, HHT, THH, THT\}$). Then $P(E_1) = P(E_2) = 4/8 = 1/2$. What is the intersection of these two events (i.e. that both events occur)?²

$$P(E_1 \cap E_2) = P(\{HHH, HHT\}) = 2/8 = 1/4 = (0.5) \cdot (0.5) = P(E_1) \cdot P(E_2)$$

Independent Events

Two events are independent (such as $E_1$ the first toss and $E_2$ the second toss) iff $P(E_1 \cap E_2) = P(E_1) \cdot P(E_2)$.

Likewise, if $E_3$ is the event where the third toss results in heads, then since all these events are independent of each other, then

$$P(E_1 \cap E_2 \cap E_3) = P(\{HHH\}) = P(E_1) \cdot P(E_2) \cdot P(E_3) = (0.5)^3 = 0.125$$

Example of a Dependent event?

Let $E$ be the (complex) event $\{HHT, THH\}$ (i.e. the first and second coins land heads and the third lands tails or, the first lands tail and the second and third heads). Thus, $P(E) = 2/8 = 1/4$.

$$E_2 \cap E\ = \{HHH, HHT, THH, THT\} \cap\{HHT, THH\} = \{ HHT, THH\}$$

$$P(E_2 \cap E) = P(\{ HHT, THH\}) = \frac{1}{4} \;\;\;\neq\;\;\; \frac{1}{8} = \frac{1}{2} \cdot \frac{1}{4} = P(E_2)\cdot P(E)$$

Since $P(E_2 \cap E) \;\neq\; P(E_2)\cdot P(E)$ these events are dependent.

Example

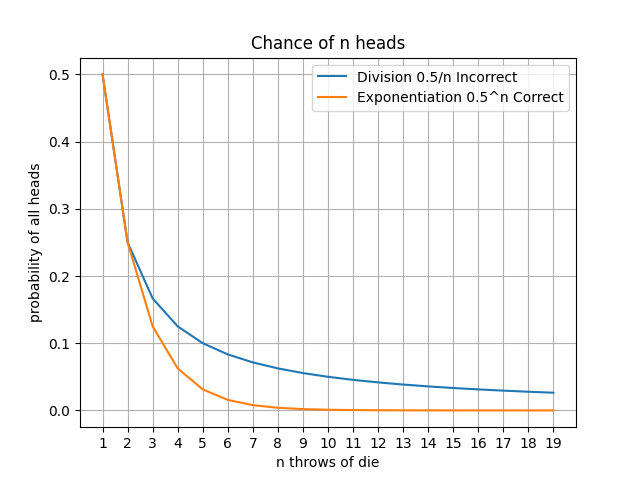
On the assumption that any throw $X$ of the coin is independent of any other throw $Y$, i.e. $P(X \cap Y) = \emptyset$, the chance of 10 heads is not $0.5/10$, i.e. a $5\%$ probability — rather, it is $0.5^{10}$, or a probability of about $0.1\%$.³

As shown in the graph below, at first, division and exponentiation are almost the same. Then, quite dramatically as $n$ increases, exponentiation quickly approaches zero.

Python for graphing

The Python code to generate the graphs is as follows:

# probability.py
from typing import List
import matplotlib.pyplot as plt

def division(n: List[int]) -> List[float]:
    # precondition for division 0.5/i
    assert n[0] >= 1 #avoid division by zero
    assert all(n[i] <= n[i+1] for i in range(len(n)-1))  # sorted

    list = []
    for i in n:
        list.append(0.5/i)
    return list

def exponentiation(n: List[int]) -> List[float]:
    # precondition for exponentiation (0.5)**i
    assert n[0] >= 1 # avoid division by zero
    assert all(n[i] <= n[i+1] for i in range(len(n)-1))  # sorted

    list = []
    for i in n:
        list.append((0.5)**i)
    return list

def plotter():
    # Create a figure containing an x/y axis
    fig, axis = plt.subplots()
    # Plot probability of all heads for n throws of the die
    # Setting title and label for x and y axes.
    axis.set(xlabel='n throws of die', ylabel='probability of all heads',
           title='Chance of n heads')
    axis.grid()   # Adding grids

    # x-axis is a List[int], i.e. of dice throws
    n = list(range(1, 20))
    plt.xticks(n) # Make x axis integers

    plt.plot(n, division(n))
    plt.plot(n, exponentiation(n))
    plt.legend(["Division 0.5/n Incorrect", "Exponentiation 0.5^n Correct"])
    fig.savefig("heads.svg") # or png
    plt.show()

# plotter() #<== uncomment to run

Factorial

In mathematics, the factorial of a positive integer $n$, denoted by $n!$, is the product of all positive integers less than or equal to n, i.e.

$$n!=n\cdot (n-1)\cdot (n-2)\cdot (n-3)\cdot \cdots \cdot 3\cdot 2\cdot 1$$

For example, $5!=5\cdot 4\cdot 3\cdot 2\cdot 1=120$. The value of $0!$ is 1, according to the convention for an empty product. In Python, we may use a built-in library or code our own function.

import math

print("Math librray: ",math.factorial(5))

def factorial(n:int) -> int:
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

print("Factorial function:",factorial(5))

Example

Consider a set of 3 people {A, B, C}. In how many ways can we order them?

1. ABC
2. ACB
3. BAC
4. BCA
5. CAB
6. CBA

For 3 people, there are $3! = 3 \cdot 2 \cdot 1 = 6$ ways of ordering them. This is because there are 3 ways of selecting the first person, then 2 ways of selecting the third person, and finally only one way of selecting the third person.

Permutations

Consider a set of 8 people {A, B, C, D, E, F, G, H}. ⁴

1. Alice
2. Bob
3. Charlie
4. David
5. Eve
6. Frank
7. George
8. Horatio

How many ways can we award a 1st, 2nd and 3rd place prize among eight contestants? (Gold / Silver / Bronze)?

We’re going to use permutations since the order we hand out these medals matters. Here’s how it breaks down:

1. Gold medal: 8 choices: A B C D E F G H. Let’s say A wins the Gold.
2. Silver medal: 7 choices: B C D E F G H. Let’s say B wins the silver.
3. Bronze medal: 6 choices: C D E F G H. Let’s say C wins the bronze.

We picked certain people to win, but the details don’t matter: we had 8 choices at first, then 7, then 6. The total number of options was $8 \cdot 7 \cdot 6 = 336$.

Let’s look at the details. We had to order 3 people out of 8. To do this, we started with all options (8) then took them away one at a time (7, then 6) until we ran out of medals.

We know the factorial is: $8! = 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$

Unfortunately, that does too much! We only want 8 · 7 · 6. How can we “stop” the factorial at 5?

We want to get rid of 5 · 4 · 3 · 2 · 1. What’s another name for this? 5 factorial!

So, if we do $8!/5!$ we get:

$$\frac{8!}{5!} = \frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 8 \cdot 7 \cdot 6$$

And why did we use the number 5? Because it was left over after we picked 3 medals from 8. So, a shorter way to write this would be:

$$\frac{8!}{(8-3)}!$$

where $8!/(8-3)!$ is just a fancy way of saying “Use the first 3 numbers of 8!”. If we have $n$ items total and want to pick $k$ in a certain order, we get:

$$\frac{n!}{(n-k)!}$$

And this is the fancy permutation formula: You have $n$ items and want to find the number of ways $k$ items can be ordered:

$$P(n,k) = \frac{n!}{(n-k)!}$$

Python for permutations

As of Python3.8, we can generate the permutations and also calculate the number of permutations (and combinations) as follows:

# permutation.py
# permutations and combinations using library functions  
from itertools import permutations 
from math import factorial

# Get all permutations of [1, 2, 3]  
perm = permutations(["A", "B", "C"])  

# Print the obtained permutations  
for i in list(perm):  
    print (i)  

# Return number of ways of obtaining a sequence of k elements 
# from a set of n elements  
def permutation(n:int, k = 2) -> int: 
    assert n >= 0 and k >= 0 
    permutations = factorial(n) / factorial(n - k)
    return round(permutations)

# Return number of ways of picking k unordered outcomes
# (a subset of k itmes) from a set of n items
def combination(n:int, k = 2) -> int: 
    assert n >= 0 and k >= 0 
    combinations = factorial(n) / ((factorial(n - k)) * factorial(k))
    return round(combinations)

print("permutation(8,3):", permutation(8, 3))
print("combination(8, 3):", combination(8, 3))****

This results in:

('A', 'B', 'C')
('A', 'C', 'B')
('B', 'A', 'C')
('B', 'C', 'A')
('C', 'A', 'B')
('C', 'B', 'A')
permutation(8,3): 336
combination(8, 3): 56

Combinations

In combinations, order doesn’t matter. Suppose we can’t afford separate Gold, Silver and Bronze medals, only empty tin cans. How many ways can we give 3 tin cans to 8 people?

In this case, the order we pick people doesn’t matter. If we give a can to Alice, Bob and then Charlie, it’s the same as giving to Charlie, Alice and then Bob. Either way, they’re equally disappointed.

This raises an interesting point — we’ve got some redundancies here. "Alice Bob Charlie" = "Charlie Bob Alice".

In terms of permutations, we have 3 choices for the first person, 2 for the second, and only 1 for the last. So we have 3 · 2 · 1 ways to re-arrange 3 people. So, if we have 3 tin cans to give away, there are 3! or 6 variations for every choice we pick. So there are 6 redundancies for each group of 3 people.

If we want to figure out how many combinations we have, we just create all the permutations and divide by all the redundancies. In our case, there are 336 permutations (from above), which we now divide by the 6 redundancies for each permutation — and get 336/6 = 56.

The general formula for $C(n,k)$ (which means “find all the ways to pick k people from n, and divide by the k! variants”):

$$C(n,k) = \frac{P(n,k)}{k!} = C(n,k) = \frac{n!}{(n-k)!k!}$$

So $C(n,k)$ is the number of ways to combine $k$ items from a set of $n$:

Birthday Paradox

We are finally ready to tackle the Birthday Problem. In a room of people, at what number $n$ of people in the room is there’s a 50-50 chance of at least two people having the same birthday?

Suppose there are only 2 people in the room. The chance of this one pair having a different birthday is:

$$1 - \frac{1}{365} \;\;=\;\ \frac{364}{365} = .997260$$

When comparing one person's birthday to another, in 364 out of 365 scenarios they won't match over $99\%$ of the time. Our chance of getting a single miss is pretty high (99.726%). The form of the left hand side of the above equation is part of a theorem of probability that follows from its axioms.

When we take the chance of pairs not having the same birthday hundreds of times, the odds of keeping up that streak drop fast. With 3 people in the room, how many pairs are there?

$$\textrm{no. of pairs of 3 people} = C(3, 2) = \frac{3!}{(3-2)! \cdot 2!} = 3$$

If the people in the room are A, B and C, then the 3 combinations of pairs $C(3, 2)$ are AB, BC and CA (where the order does not matter, e.g. AB is the same as BA).

With 5 people in the room there are $C(5,2) = 10$ pairs. By making 10 birthday comparisons (one for each pair of 2) and having them all be different is like getting heads 10 times in a row -- we had to dodge "tails" each time. The probability of 5 people in a room not sharing the same birthday is:

$$\left(\frac{364}{365}\right)^{C(5,2)} \;=\;\; \left(\frac{364}{365}\right)^{10}$$

Thus, the probability $p(5)$ of 5 people sharing the same birthday is:

$$p(5) \;\;=\;\; 1 - \left(\frac{364}{365}\right)^{C(5,2)} \;=\;\; 1 - \left(\frac{364}{365}\right)^{10}$$

Theorem of the the Complement of an an Event

Suppose that $A$ is an event in the sample space $S$, and $A^c$ is the complement of the subset $A$ (i.e. $A^c$ is the set of all elements in $S$ that are not $A$; or formally, $A^c = \{x \in S | x \notin A\}$). Then:

$$P(A^c) = 1 - P(A)$$

Generalizing this formula to $n$ people in the room, we obtain

$$p(n) \;\;=\;\; 1 - \left(\frac{364}{365}\right)^{C(n,2)} \;=\;\; 1 - \left(\frac{364}{365}\right)^{n(n-1)/2}$$

where $p(n)$ is the probability of $n$ people in a room sharing the same birthday.

Formula for a 50% probability (or more) of not sharing a birthday

$$1 - \left(\frac{364}{365}\right)^{C(n,2)} \;\;\geq\;\; 0.5$$

We must find the least number of people $n$ to make the above inequality true.

Python

We will use Python to calculate and plot the least number of people $n$ to make the above inequality true. Below is a useful plot generated by our Python code.

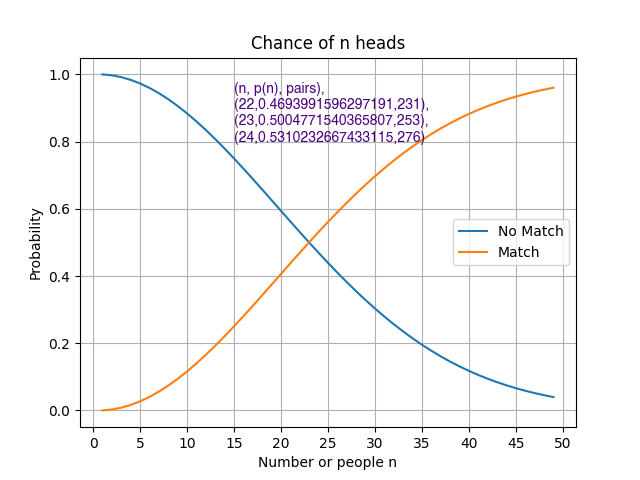
The plot shows that at $n = 23$, the probability $p(n)$ is about $0.5$. For 23 people, there are 253 combinations of pairs that produce the match probability of about $0.5\%$.

#!/usr/bin/env python3
# birthday.py
from math import comb, ceil, floor
from typing import List, Tuple
import matplotlib.pyplot as plt
# import numpy as np

def no_match(n:int) -> float:
    # probability of n people having different birthdays
    return (364/365)**comb(n,2)

def match(n:int) -> float:
    # probability of n people having same birthdays
    return (1 - no_match(n))

# needed for plots to hide some ticks; default reveal every 5th step
def computeTicks (x: List[float], step = 5):
    """
    Computes domain with given step encompassing series x
    @ params
    x    - Required - A list-like object of integers or floats
    step - Optional - Tick frequency
    """
    xMax, xMin = ceil(max(x)), floor(min(x))
    dMax, dMin = xMax + abs((xMax % step) - step)\
        + (step if (xMax % step != 0) else 0), xMin - abs((xMin % step))
    return range(dMin, dMax, step)

match49: Tuple[int, float, int] # n, p(n), no. of pairs
match50: Tuple[int, float, int] # 50% version
match51: Tuple[int, float, int] # more than 50%

def matches2str() -> str:
    # string representation of match49,50,51 for plot
    l=[match49, match50, match51]
    s="(n, p(n), pairs),"
    for t in l:
        s = (s + '\n' + "(%s,%s,%s),") % t
    s = s[:-1]
    return s

# font for matches2str on plot
font = {'family': 'Helvetica',
        'color':  'indigo',
        'weight': 'normal',
        'size': 10,
        }

matches:    List[float] = []  # matches[n-1] is p(n)
no_matches: List[float] = []  # no_matches[n-1] is 1-p(n)

# populate matches and no_matches for plot
# also calculate match49,50,51
def make_matches(input: List[int]) -> None:
    # precondition for matches of a list of people
    assert input[0] >= 1 # avoid division by zero
        #sorted
    assert all(input[i] <= input[i+1] for i in range(len(input)-1))

    global matches, no_matches
    matches = []; no_matches = []
    global match49, match50, match51
    # match49 = 0; match50 = 0; match51 =0
    for n in input:
        no_matches.append(no_match(n))
        matches.append(match(n))
        if (0.498 <= match(n) and match(n) <= 0.502):
            match49 = (n-1, match(n-1), comb(n-1,2))
            match50 = (n, match(n), comb(n, 2))
            match51 = (n+1, match(n+1), comb(n+1, 2))

def plotter():
    # x-axis is a List[int], i.e. of people
    xaxis = list(range(1,50,1))

    make_matches(xaxis)
    # print(matches)
    # Create a figure containing an x/y axis
    fig, axis = plt.subplots()
    # Plot probability of all heads for n throws of the die
    # Setting title and label for x and y axes.
    axis.set(xlabel='Number or people n', ylabel='Probability',
           title='Chance of n heads')
    axis.grid()   # Adding grids
    plt.xticks(xaxis) # Make x axis integers
    # plot matches and no_matches
    plt.plot(xaxis, no_matches)
    plt.plot(xaxis, matches)
    # show very 5 ticks of x axis
    plt.xticks(computeTicks(xaxis,5))
    plt.legend(["No Match", "Match"])
    # place text on plot of match49,50,51
    s: str = matches2str()
    plt.text(15, 0.8, s, fontdict=font)

    fig.savefig("matches.svg") # or png
    plt.show()
    print(match49,match50,match51)

if __name__ == "__main__":
    plotter()

---

1. See Birthday Paradox ↩

2. Informally $P(A \cap B)$ means $P(A \textrm{ occurs and } B \textrm{ occurs})$. Also, $P(A \cup B)$ means $P(A \textrm{ occurs or } B \textrm{ occurs})$ ↩

3. Note that in 10 throws of the die, there are $2^{10}$ possibilities (e.g. HTTTTTTTTT is one possibility, TTTTTTTTTH is another possibility etc.). Furthermore, $(1/2)^{10} = 0.5^{10} = 0.0009765625 \approx 0.1\%$. ↩

4. See Permutations and Combinations ↩