5 The normal probability density function

Perhaps the most commonly used probability distribution in science and engineering is the normal probability density function, often called the bell curve. The figure below shows three examples of the normal probability density function for different values of the mean \(\mu\) of the distributions; the peak of a bell curve occurs at the mean value \(\mu\).

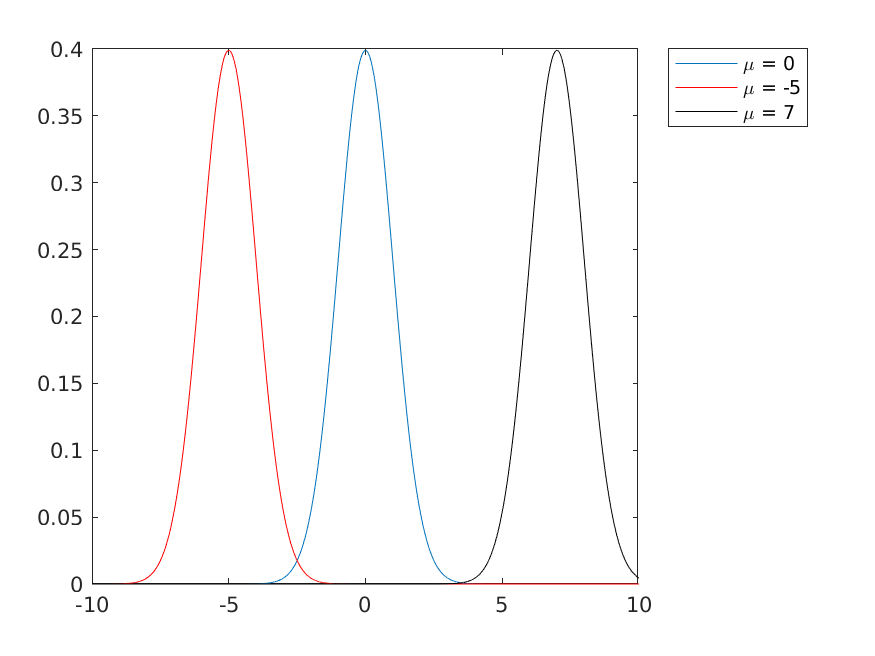
Three normal probability density functions having different mean values.

Figure 5.1: Three normal probability density functions having different mean values.

The equation of the normal distribution shown in the figure above is given by:

\[y = \frac{1}{\sqrt{2 \pi}} e^{-0.5 (x - \mu) ^ 2}\]

In MATLAB open the file named normPDF.m. This file contains a function that when completed returns the value of the function shown above.

Complete the function so that it returns the value y as defined by the equation above.

The MATLAB function exp can be used to compute the value of \(e^x\). Review the help documentation for the method to determine how to use it correctly.

The MATLAB function sqrt can be used to compute the value of \(\sqrt{x}\). Review the help documentation for the method to determine how to use it correctly.

5.1 Using normPDF.m

Test your function by typing the following in the MATLAB Command Window:

x = 1;
mu = 0;
y = normPDF(x, mu)

A correct function would cause the value 0.2420 to be output. If the correct value is not output, review your function and correct any errors that you find.

For values of \(x\) that are far away from the mean of the distribution, the function should return a value that is approximately equal to zero; for example, if we have a normal probability density function with mean \(\mu = 0\) then evaluating the function at \(x = 100\) should produce a value of zero:

y = normPDF(100, 0)

5.2 Solve a simple problem using normPDF.m

Consider the following two facts about the normal distribution:

  1. The maximum value of the normal probability density function occurs when \(x = \mu\).
  2. The probability density function is symmetric about the mean; that is the density function evaluated at \(x = \mu - a\) is equal to the density function evaluated at \(x = \mu + a\) for any value of \(a\)

In MATLAB, open the script file maxMinusPlus.m. Complete the script so that it does the following:

  1. Computes the maximum value of the normal probability density function. Store the maximum value in a variable named maxVal. Choose any value of \(\mu\) where \(-100 < \mu < 100\); you should always get the same result.
  2. Computes two values of the normal probability density function evaluated at \(x = \mu - 2\) and \(x = \mu + 2\). Store the values in two variables name minus and plus.

Your script must use the function normPDF that you created earlier.