Research
My research interests are in the area of computer-assisted surgery: image processing, image registration, visualization, surgical planning, error analysis, and applications of computer assistance in orthopaedic surgery.
Line-Based Ultrasound Calibration
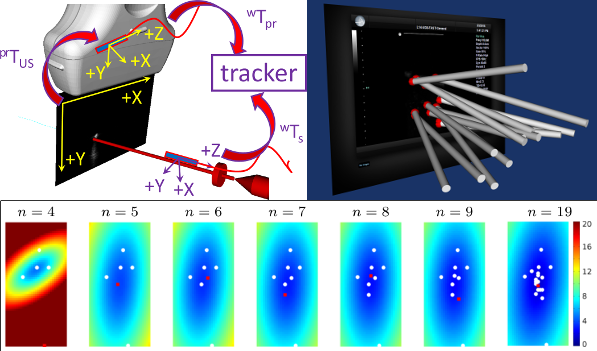 We present an ultrasound calibration framework that is guided
by the prediction of target registration error (TRE). Between successive measurements of
the calibration phantom, our algorithm predicts how to position and orient the calibration
phantom to collect the subsequent ultrasound fiducial to maximize the minimization of the
predicted TRE. To accomplish this, we first introduced an oriented-line calibration phantom
and modelled the ultrasound calibration process as a point-to-line iterative closest point
registration problem. We then derived a spatial stiffness model for point-to-line registration.
Assuming the fiducial localization error is isotropic and identical, the spatial stiffness model
estimates the TRE for each pixel based on the current calibration estimate. We then search
through the calibration tool space to find the pose (orientation and position) that, if the next
fiducial is to be collected at this pose, the TRE is maximally minimized. Both the simulation
and experimental results suggest that TRE decreases monotonically, reaching an asymptote
when more than 12 measurements are made. Independent point reconstruction accuracy
assessment showed sub-millimeter accuracy of the proposed calibration framework.
We present an ultrasound calibration framework that is guided
by the prediction of target registration error (TRE). Between successive measurements of
the calibration phantom, our algorithm predicts how to position and orient the calibration
phantom to collect the subsequent ultrasound fiducial to maximize the minimization of the
predicted TRE. To accomplish this, we first introduced an oriented-line calibration phantom
and modelled the ultrasound calibration process as a point-to-line iterative closest point
registration problem. We then derived a spatial stiffness model for point-to-line registration.
Assuming the fiducial localization error is isotropic and identical, the spatial stiffness model
estimates the TRE for each pixel based on the current calibration estimate. We then search
through the calibration tool space to find the pose (orientation and position) that, if the next
fiducial is to be collected at this pose, the TRE is maximally minimized. Both the simulation
and experimental results suggest that TRE decreases monotonically, reaching an asymptote
when more than 12 measurements are made. Independent point reconstruction accuracy
assessment showed sub-millimeter accuracy of the proposed calibration framework.
Line-Based Target Registration Error
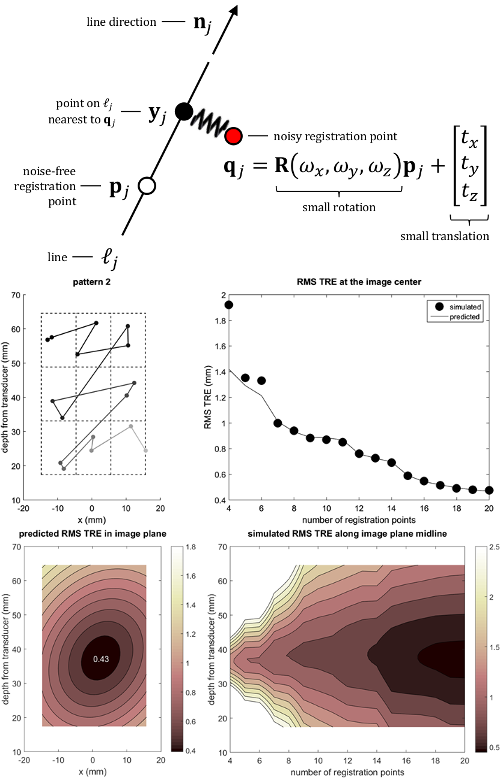 We present a novel method for estimating target registration error (TRE) in point-to-line registration. We develop a spatial
stiffness model of the registration problem and derive the stiffness matrix of the model which leads to an analytic expression
for predicting the root-mean-square (RMS) TRE. Under the assumption of isotropic localization noise, we show that the
stiffness matrix for line-based registration is equal to the difference of the stiffness matrices for fiducial registration and
surface-based registration. The expression for TRE is validated in the context of freehand ultrasound calibration performed
using a tracked line fiducial as a calibration phantom. Measurements taken during calibration of a tracked linear ultrasound
probe were used in simulations to assess TRE of point-to-line registration and the results were compared to the values
predicted by the analytic expression. The difference between predicted and simulated RMS TRE magnitude for targets near
the centroid of the registration points was less than 5% of the simulated magnitude when using more than 6 registration
points. The difference between predicted and simulated RMS TRE magnitude for targets over the entire ultrasound image
was almost always less than 10% of the simulated magnitude when using more than 10 registration points. TRE magnitude
was minimized near the centroid of the registration points and the isocontours of TRE were elliptic in shape.
We present a novel method for estimating target registration error (TRE) in point-to-line registration. We develop a spatial
stiffness model of the registration problem and derive the stiffness matrix of the model which leads to an analytic expression
for predicting the root-mean-square (RMS) TRE. Under the assumption of isotropic localization noise, we show that the
stiffness matrix for line-based registration is equal to the difference of the stiffness matrices for fiducial registration and
surface-based registration. The expression for TRE is validated in the context of freehand ultrasound calibration performed
using a tracked line fiducial as a calibration phantom. Measurements taken during calibration of a tracked linear ultrasound
probe were used in simulations to assess TRE of point-to-line registration and the results were compared to the values
predicted by the analytic expression. The difference between predicted and simulated RMS TRE magnitude for targets near
the centroid of the registration points was less than 5% of the simulated magnitude when using more than 6 registration
points. The difference between predicted and simulated RMS TRE magnitude for targets over the entire ultrasound image
was almost always less than 10% of the simulated magnitude when using more than 10 registration points. TRE magnitude
was minimized near the centroid of the registration points and the isocontours of TRE were elliptic in shape.
Point-Based Target Registration Error
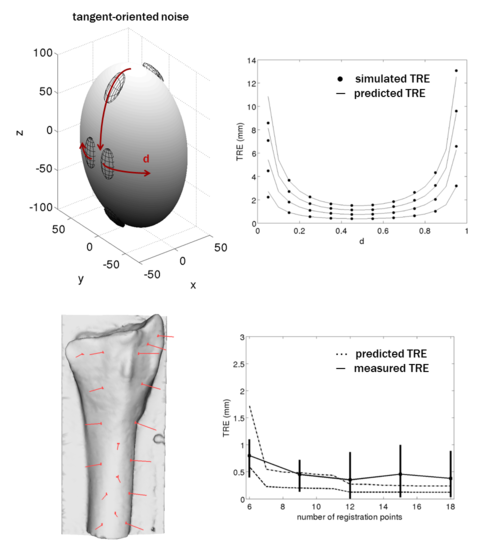 Guidance systems used for image guided surgery register data collected in real time
(i.e. the position of a hand-held probe) to preoperative images to help guide a minimally
invasive surgery. In the process of registration, the distances between corresponding points,
representing the target registration error (TRE), is the most important error measure.
Guidance systems used for image guided surgery register data collected in real time
(i.e. the position of a hand-held probe) to preoperative images to help guide a minimally
invasive surgery. In the process of registration, the distances between corresponding points,
representing the target registration error (TRE), is the most important error measure.
Finding TRE with noisy data points
Data points that are collected will each have a corresponding noise. Given the task of registering
these noisy points to a rigid body, to estimate the root mean square target registration error, we
came up with an analytic equation.
To then test the accuracy of this equation, we ran numerous registration simulations using both synthetic
and real data points and models. The synthetic model was that of an ellipsoid, and random noise was added
to points drawn from the surface of the ellipsoid. For the measured data points, we used plastic bone replicas
and an optical tracking system. After gathering many data points on the bone using the tracking system, we
performed registration of these points onto a 3D model of the plastic bones, which was produced with a CT scan.
Individualized Instrumentation for Distal Radius Osteotomy
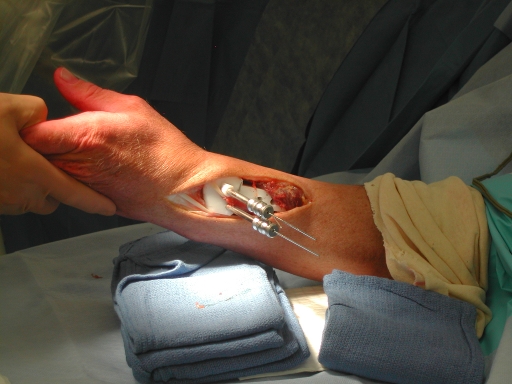 The radius is the most commonly fractured bone in the arm. In cases where
the fractured radius heals in an abnormal position, surgical treatment
may be required to correct the deformity and restore the function of
the wrist joint. Distal radius osteotomy involves cutting the radius
near the original fracture site, rotating and translating the distal
fragment to restore normal radiograpic alignment, filling the resulting
gap with bone graft or substitute, and then securing the assembly with
a metal plate and screws. In conventional technique, the alignment
is achieved under fluoroscopic (x-ray) guidance. We've designed and
tested a 3D printed indvidualized guide that fits onto to the
patient's radius and provides navigational guidance of the fixation
screws so that when the radius is cut and plated the pre-drilled
holes align to the holes in the fixation plate.
The radius is the most commonly fractured bone in the arm. In cases where
the fractured radius heals in an abnormal position, surgical treatment
may be required to correct the deformity and restore the function of
the wrist joint. Distal radius osteotomy involves cutting the radius
near the original fracture site, rotating and translating the distal
fragment to restore normal radiograpic alignment, filling the resulting
gap with bone graft or substitute, and then securing the assembly with
a metal plate and screws. In conventional technique, the alignment
is achieved under fluoroscopic (x-ray) guidance. We've designed and
tested a 3D printed indvidualized guide that fits onto to the
patient's radius and provides navigational guidance of the fixation
screws so that when the radius is cut and plated the pre-drilled
holes align to the holes in the fixation plate.
Distraction Osteogenesis with a Taylor Spatial Frame
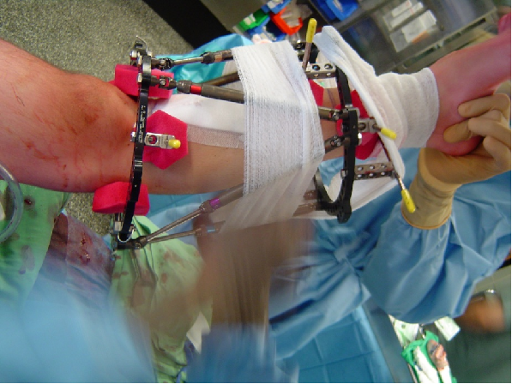 Rotational and translational deformities in the long bones can be corrected
using distraction osteogenesis, developed by Russian orthopaedic surgeon
Gavril Ilizarov. Ilizarov's method is based on the biological principle of
inducing new bone growth by gradually distracting a fracture at regular
intervals. More specifically, the method is achieved by performing a
corticotomy or osteotomy on the deformed bone, fixating the distressed
bone with a mechanical fixator, and distracting the bone according to a
set schedule of corrections.
We have developed a computer-assisted technique
that modifies the conventional approach to deformity
correction, using the Ilizarov method in four fundamental
ways. (1) The need for the surgeon to preoperatively compute
the frame parameters is removed.
(2) The performed correction is based on the actual
location of the frame with respect to the anatomy;
any translational or angular malalignments that occur
while mounting the frame are compensated for
immediately, thereby potentially removing the need
for residual correction.
(3) The correction is calculated based on 3D coordinates
from CT data, rather than measured from radiographs.
(4) The surgeon has flexibility in frame placement;
hence, anatomical constraints that may not have been
apparent preoperatively can be compensated for in
surgery.
Rotational and translational deformities in the long bones can be corrected
using distraction osteogenesis, developed by Russian orthopaedic surgeon
Gavril Ilizarov. Ilizarov's method is based on the biological principle of
inducing new bone growth by gradually distracting a fracture at regular
intervals. More specifically, the method is achieved by performing a
corticotomy or osteotomy on the deformed bone, fixating the distressed
bone with a mechanical fixator, and distracting the bone according to a
set schedule of corrections.
We have developed a computer-assisted technique
that modifies the conventional approach to deformity
correction, using the Ilizarov method in four fundamental
ways. (1) The need for the surgeon to preoperatively compute
the frame parameters is removed.
(2) The performed correction is based on the actual
location of the frame with respect to the anatomy;
any translational or angular malalignments that occur
while mounting the frame are compensated for
immediately, thereby potentially removing the need
for residual correction.
(3) The correction is calculated based on 3D coordinates
from CT data, rather than measured from radiographs.
(4) The surgeon has flexibility in frame placement;
hence, anatomical constraints that may not have been
apparent preoperatively can be compensated for in
surgery.