4 Functions [10 marks]
Consider the triangle shown below:
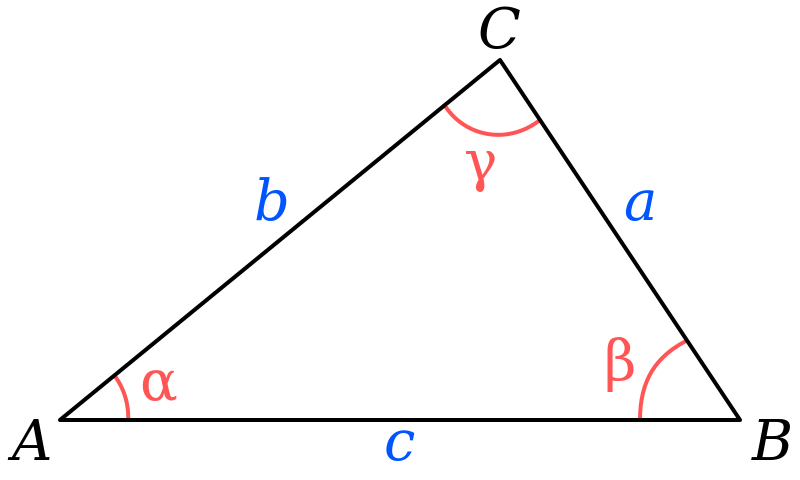
The Law of Cosines can be used to find the angles \(\alpha\), \(\beta\), and \(\gamma\) if the lengths of the three sides are known. The angles in degrees are given by:
\[\begin{eqnarray*} \alpha & = & \arccos \left(\frac{b^2 + c^2 - a^2}{2bc} \right)\\ \beta & = & \arccos \left(\frac{a^2 + c^2 - b^2}{2ac} \right)\\ \gamma & = & 180^\circ - \alpha - \beta \end{eqnarray*}\]The function \(\arccos (x)\) is the inverse cosine function (often written as \(\cos^{-1}(x)\)). See help acos and help acosd for the corresponding MATLAB function.
Create a function that uses the three formulas given above to compute the angles \(\alpha\), \(\beta\), and \(\gamma\) in degrees given the lengths \(a\), \(b\), and \(c\).
Your function should satisfy the following constraints:
- it should be named
angles - it should return three values
alpha,beta, andgamma(the three angles of the triangle) - it should have three input values
a,b, andc(the lengths of the sides of the triangle shown in the figure above).
4.1 Example usage
[alpha, beta, gamma] = angles(3, 4, 5)