CSE1030 Lab 9

Introduction

This lab has you traverse a recursive data structure called a binary search tree. You should review the Section E lecture slides before attempting this lab.

This lab is optional. Your lab grade will be computed using the 8 highest grades from the 9 labs.

Binary Search Trees

A binary search tree is a tree where each node has at most two child nodes (usually called the "left" child node and the "right" child node). The left child is the root of the left subtree and the right child is the root of the right subtree. Each node contains a data element, and the nodes of the tree are arranged according to the following 3 rules:

1. all of the nodes in the left subtree have data elements that are less than the data element of the root node
2. all of the nodes in the right subtree have data elements that are greater than or equal to the data element of the root node
3. rules 1 and 2 apply recursively to every subtree

The structure of the binary search tree supports efficient sorting of and searching for elements in the tree. A variation of the binary search tree called a red-black tree is used to implement Java's TreeSet and TreeMap data structures.

An example of a binary search tree of three elements is shown in the figure below:

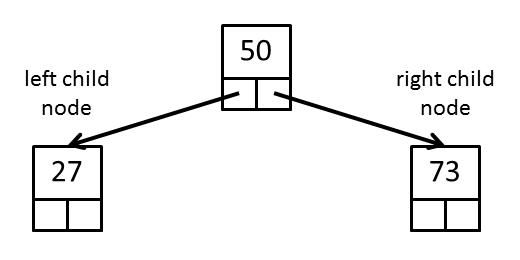
In this tree there is a root node with a data element of 50. The left child node has a data element of 27 (27 < 50). The right child node has a data element of 73 (73 ≥ 50).

An example of a binary search tree of eight elements is shown in the figure below:

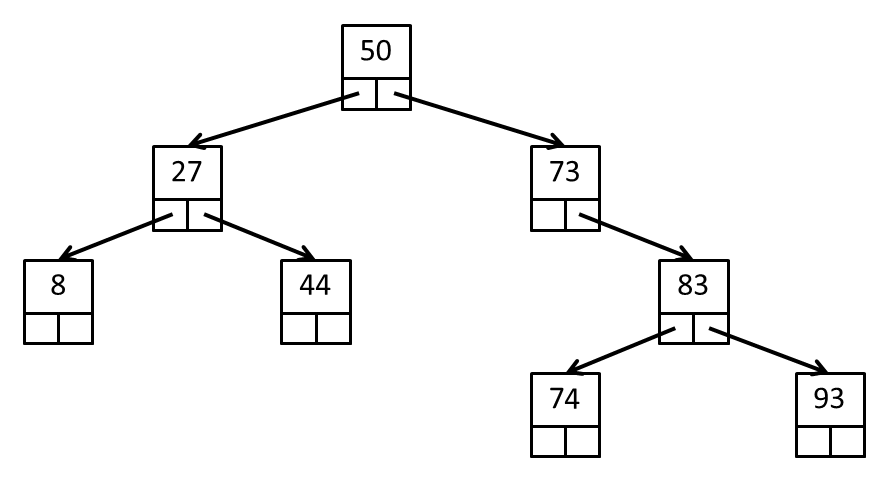
In this tree there is a root node with a data element of 50. The data elements of all of the nodes in the left subtree of the root are less than 50. The data elements of all of the nodes in the right subtree of the root are greater than or equal to 50.

If we examine the subtree rooted at the node with data element 27, we see that rules 1 and 2 apply recursively to this subtree: the left child node has a data element of 8 (8 < 27) and the right child node has a data element of 44 (44 ≥ 27).

Similarly, if we examine the subtree rooted at the node with data element 73, we see that rules 1 and 2 apply recursively to this subtree: all of the nodes below the root node of 73 have data values less than or equal to 73.

Adding an element to a binary search tree

The recursive structure of the binary search tree leads to recursive algorithms that operate on the tree. Consider adding an element to a binary search tree; for example suppose that we want to add the element 19 to the previous tree:

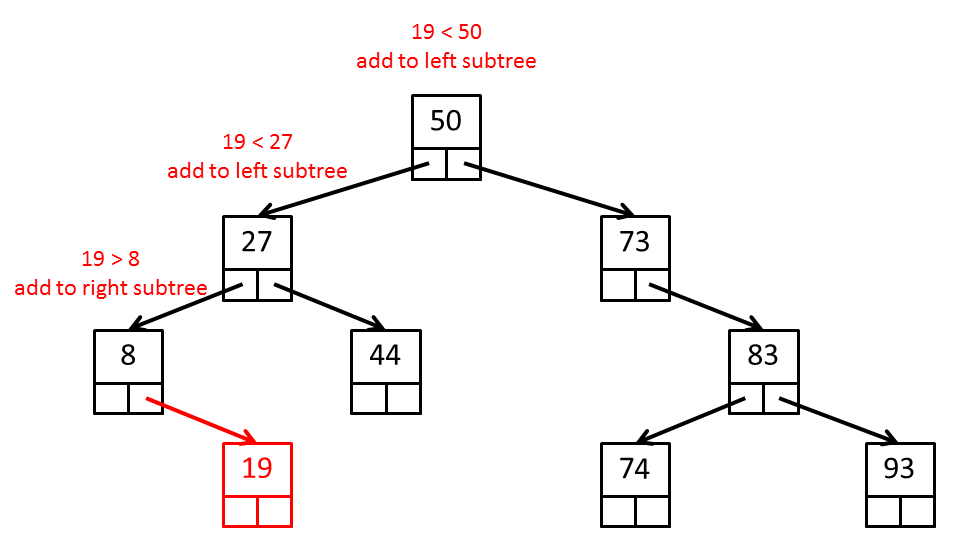
If there is a root node, we compare the element 19 with the data in the root node; because 19 is less than 50, we know that the element must be added to the left subtree. We now examine the left subtree that is rooted at the node with data element 27; because 19 is less than 27, we know that the element must be added to the left subtree. We now examine the left subtree that is rooted at the node with data element 8; because 19 is greater than or equal to 8, we know that the element must be added to the right subtree. Because the right subtree is empty, we create a new node with data element 19 and set the right child node to the new node.

Traversing the tree: Inorder traversal

A traversal of a tree visits all of the nodes of the tree exactly once in a systematic fashion. Because of the branching structure, a binary tree can be traversed in many different ways.

For a binary search tree, the inorder traversal visits the nodes in sorted order of the data elements. For example, the inorder traversal of the tree shown above would visit the nodes in the following order: {8, 19, 27, 44, 50, 73, 74, 83, 93}. The inorder traversal can be expressed recursively starting at the root node as:

1. traverse the left subtree
2. visit the root
3. traverse the right subtree

The toString method in BinarySearchTree implements a recursive inorder traversal.

Traversing the tree: Preorder traversal

The preorder traversal of a tree can be expressed recursively starting at the root node as:

1. visit the root
2. traverse the left subtree
3. traverse the right subtree

The preorder traversal of the tree shown bove would visit the nodes in the following order: {50, 27, 8, 19, 44, 73, 83, 74, 93}.

An iterative version of the preorder traversal can be accomplished with the help of a stack:

1. push the root node onto a stack
2. while the stack is not empty
   1. pop the stack and visit the popped node
   2. push the right child of the popped node onto the stack
   3. push the left child of the popped node onto the stack

In the iterative version, you must take care to never push a null node onto the stack.

Traversing the tree: Breadth first search traversal

The breadth first search traversal of a tree visits the nodes of the tree in level order where nodes are visited from left to right on each level before proceeding to the next lower level of the tree. The breadth first search traversal of the tree shown bove would visit the nodes in the following order: {50, 27, 73, 8, 44, 83, 19, 74, 93}.

An iterative version of the breadth first search traversal can be accomplished with the help of a queue:

1. enqueue the root node
2. while the queue is not empty
   1. dequeue the front node and visit the node
   2. enqueue the left child of the node
   3. enqueue the right child of the node

In the iterative version, you must take care to never enqueue a null node into the queue.

Question 1: Complete the implementation of BinarySearchTree

Complete the implementation of BinarySearchTree. The API for all methods (private and public) can be found here:

• BinarySearchTree, Queue, and Stack APIs

Starter code can be found here:

• Queue.java
• Stack.java
• BinarySearchTree.java

You need to implement two methods to perform a preorder traversal and breadth first search traversal of the tree:

public String preOrder()

public String bfs()

You methods must be iterative: preOrder should use a stack and bfs should use a queue. Running the main method should produce the following output:

inorder             : {12, 25, 35, 40, 50, 60, 75, 85, 95}
preorder            : {50, 25, 12, 35, 40, 75, 60, 85, 95}
breadth first search: {50, 25, 75, 12, 35, 60, 85, 40, 95}

A Note on Syntax

The binary search tree implementation uses generics. In other words, we can create a tree that holds elements of any type that has a natural ordering:

BinarySearchTree<Integer> t = new BinarySearchTree<Integer>();
BinarySearchTree<String> u = new BinarySearchTree<String>();
BinarySearchTree<Date> v = new BinarySearchTree<Date>();

The tree can hold elements of any type that implements the Comparable interface. In Java, this is expressed as follows:

public class BinarySearchTree<E extends Comparable<? super E>>

E is used as the name of the type of element that the tree holds. E extends Comparable<? super E> means that the type E must also implement the Comparable interface (so that we can perform the less than and greater than or equal to comparisons using compareTo). The type E does not need to implement Comparable<E>, however. As long as E implements Comparable<T> where T is a super class of E we can still use compareTo to compare elements. The actual type T is unimportant. The syntax ? super E is used to indicate that there is some unnamed type that is a super class of E.

Submit your work

Submit your program using the command:

submit 1030 L9 BinarySearchTree.java