EECS2030 Lab 6
Fall 2017
Due date:
ALL SECTIONS: Friday Nov 24 before 23:59
Introduction
In this lab, you must implement 5 recursive algorithms. You should review the course notes and lecture slides before attempting this lab.
For Questions 1–3, you are given examples that should help
you determine the base case(s) and the recursive invocation.
For Questions 4 and 5, you need to find the base cases and recursive
invocations on your own.
Constraints: no regular expressions, loops, or methods such as "contains", "matches" or "replace*" should be used in your implementation for these methods.
You will implement methods for all Questions within the RecursiveTasks utility class. The API for this class can be found here:
Starter project can be downloaded from the following link (this includes some initial JUnit for questions 1-3. Add more test cases to be thorough:
Question 1: Return the parenthesis enclosed substring
To do this, the input string str will be recursively 'eroded' until only the string enclosed in parenthesis remains.
The string inside the parenthesis (inclusive of the parenthesis), will be returned as the output of the method.
getParenthesis("abc(xyz)st")
→ getParenthesis("bc(xyz)st") // recursive calls
→ getParenthesis("c(xyz)st")
→ getParenthesis("(xyz)st")
→ getParenthesis("(xyz)s")
→ getParenthesis("(xyz)")
→ getParenthesis("(xyz)")
→ "(xyz)" // base case "(xyz)"
Other examples of input-output pairings include:
getParenthesis("xyz(abc)") → "(abc)"
getParenthesis("(a)xy") → "(a)"
getParenthesis("xy()z") → "()"
getParenthesis("(.)1") → "(.)"
The base case occurs when the string str has an open "(" and close ")" parenthesis in both the first and last character position respectively.
Note: You cannot actually remove the last character from a string because strings are immutable;
for a string s you can obtain the substring containing all the characters of s
except the last element by using substring:
String allButLastChar = s.substring(0, s.length() - 1);
Implement the method getParenthesis(String str)
using the recursive algorithm described above.
Question 2: Count occurrences of a sub-string within a string
This method counts the number of times the substring sub occurs in a string.
To do this, the input string str will be recursively 'eroded' until the first
part of the string is sub. If so, 1 will be added to the count.
numOccurances("dogmonkeydog")
= 1 + numOccurances("monkeydog") // recursive calls
= 0 + numOccurances("onkeydog")
= 0 + numOccurances("nkeydog")
= 0 + numOccurances("keydog")
= ...
= 0 + numOccurances("dog")
= 1 // base case "dog"
Other examples of input-output pairings include:
numOccurances("dogmonkeydog","dog") will return 2
numOccurances("dogmonkeydog","mon") will return 1
numOccurances("dogmonkeydog","cow") will return 0
The base case occurs when the string str is equal to sub
or the str is smaller than sub.
Implement the method numOccurances(String str, String sub)
using the recursive algorithm described above.
Question 3: Determine if a string is nested and balanced parenthesis
This method should, when given a string, return true if it is a nesting of zero or more pairs of balanced parenthesis, like "(())" or "((()))".
If the parenthesis are unbalanced, or the string includes characters other than parenthesis, the method should return false
E.g.
parenthIsNested("(())") will return true
parenthIsNested("((()))") will return true
parenthIsNested("(((x))") will return false
The base cases are "()" or a string without parenthesis
Implement the method parenthIsNested(String str) by checking the first and last chars, and then recursing (if necessary) on what's inside.
Question 4: Create a fractal pattern from circles
Fractal patterns are self similar repeating patterns over different scales. These are often found in nature, and are often used in computer graphics to generate natural looking scenes (e.g. mountains, trees, etc.)
A fractal is defined by a spatial operation (drawing) that is defined for a given location on an image. The operation is repeated with a modification to its scale, so that the scaled down version of the pattern is drawn again, usually at a new location. The methodology for selecting a new location and repeating the drawing operation can be defined as a recursive step in the process, and this is repeated for n levels of recursion, or until some parameter in the drawing meets a terminating condition.
The following fractal for instance, is generated starting with an initial set of 4 circles, each centred on an imaginary circle of radius R [i.e. at (-R,0), (+R,0), (0,-R), and (0,+R): where the centre of the drawing is considered the origin (0,0)]. The radius (r) for each of the circles is R/2.
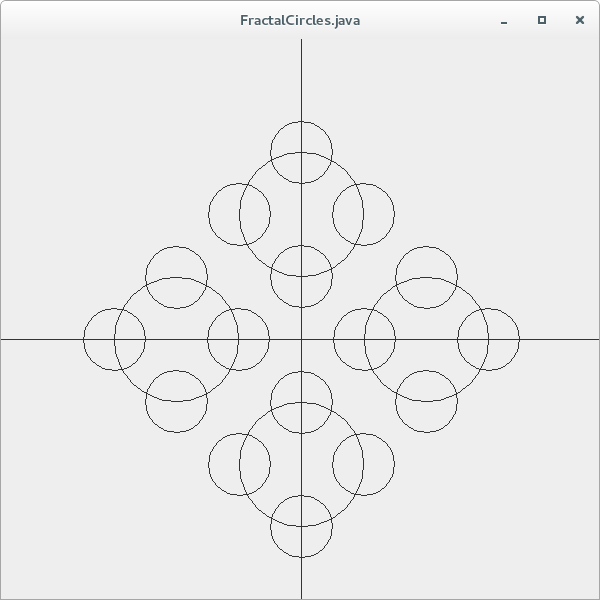
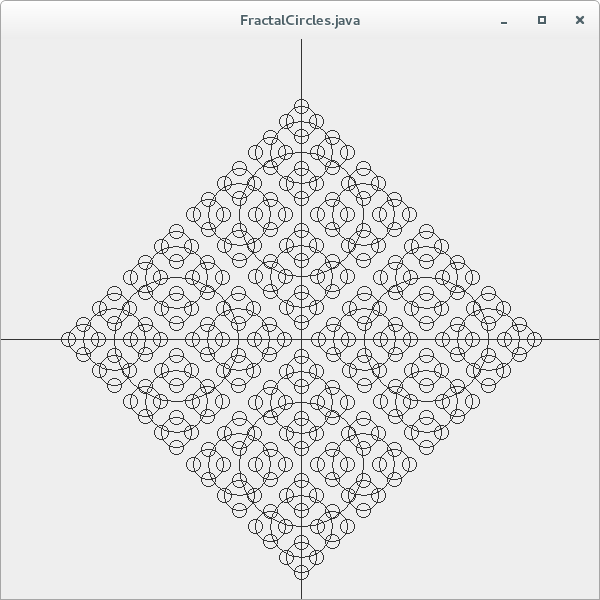
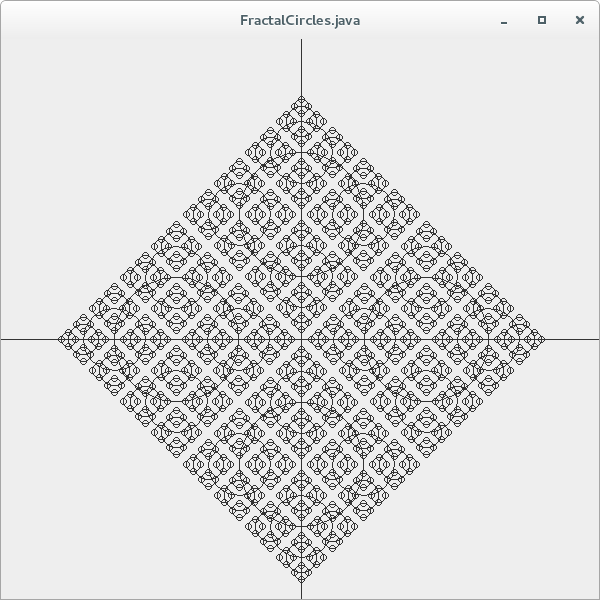
At the each level of recursion, a new set 4 circles is generated and centred on each of the circles in the initial set. For each level of recursion, R is reduced by a factor of 2. The diagram below shows the fractal at n=1, n=2, n=4 and n=5 levels of recursion respectively: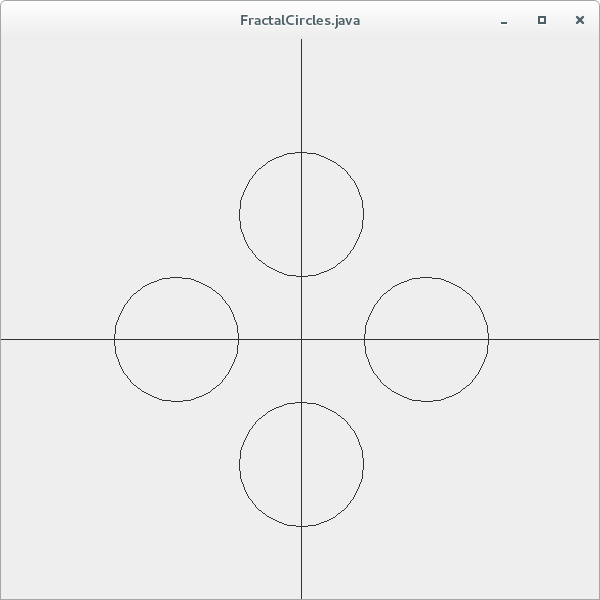
In a variation of this example, the set of 4 circles is generated, however, they are only generated and centred on the top and bottom circle from the parent set at each recursive step. This results in the following fractal pattern (shown for n=3 and n=5 levels of recursion respectively):
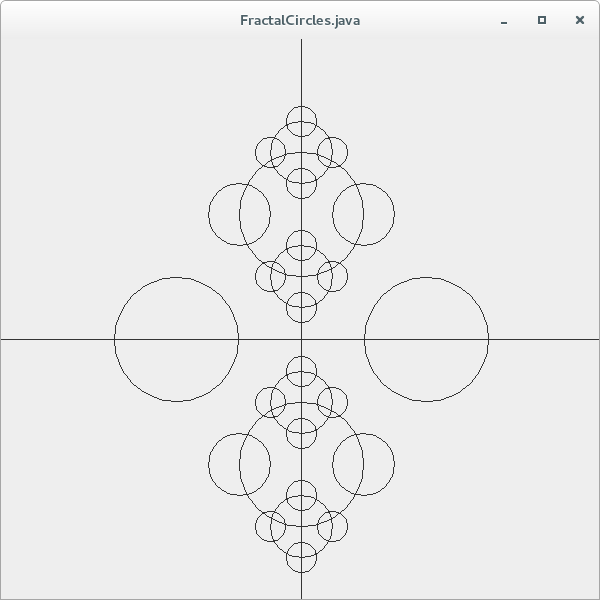
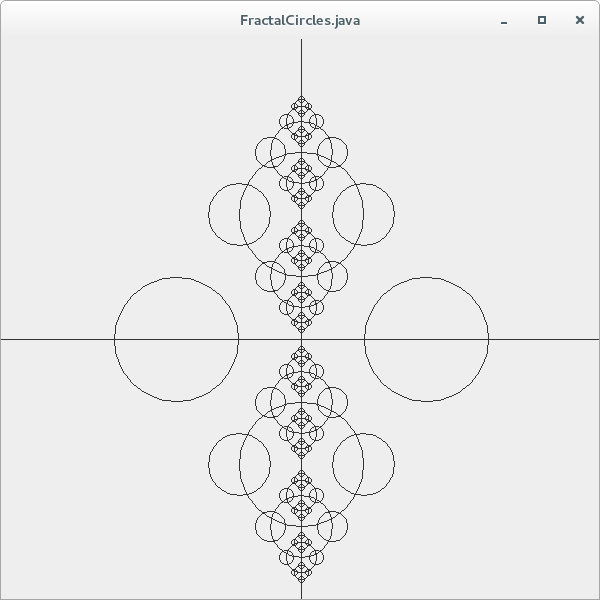
The task for Question 4, is to complete the recursive function genFractal(list, cx, cy, R, n, mode), which will compute and generate Circle objects recursively and return them in the list (a List of Circle objects).
Assume: list = reference to List(see Circle class in API); cx,cy = centre of the set of 4 circles; R = radius on which the set of 4 circles is positioned; n = recursive levels to compute (i.e. n=k will recurse k times); mode = mode of fractal pattern (defines on which circles recursion will take place) - see below
The helper classes in FractalPatterns.java take care of drawing the circles to a window. You do not need to complete anything other than the genFractal method (in your RecursiveTasks class), however you can modify the call to this method to explore and draw different types of fractal patterns.
The goal of genFractal is to create the above set of fractal patterns, as determined by the variable mode. Mode is an array of 4 boolean values, each one indicating whether or not to recursively generate the pattern of 4 circles at every circle centre, or at a subset of these. Assume that mode specifies a boolean flag representing [left, right, up, down]:
i.e.
boolean [] mode = {true,true,true,true} will generate the first fractal pattern shown above
boolean [] mode = {false,false,true,true} will generate the second fractal pattern shown above
You will need to define the base case(s) yourself. Test cases are not provided, however you should create some to evaluate that the list of Circle objects is expected. Complete the genFractal method.
Question 5: Search for a sum that equals a given target
This task involves the use of a binary search on a possible space of alternative sums that might arise from including/excluding integers from a given set. The goal is to calculate and determine if there exists a sum of (some) or all of the elements in an integer array that and test if it is equal to a given target value. If there exists such a sum, then return true, otherwise return false.
E.g. sumSome(0, [2, 4, 8], 0, 10) → true sumSome(0, [2, 4, 8], 0, 14) → true sumSome(0, [2, 4, 8], 0, 9) → false
This is a classic backtracking recursion problem, and involves a binary search step. I.e. we want to explore what sums are possible with/without each element (integer) in the set. Understanding the strategy in this problem leads to a design pattern for many problems that involve searching within a space of choices.
Rather than looking at the whole array, convention is to consider the part of the array starting at index and continuing to the end of the array. The caller can specify the whole array simply by passing start as 0. No loops are needed to complete this method, and recursive calls should progress down the array using the index variable.
Think carefully about the base case(s) and recursive step(s), and implement the method sumsome(int index, int[] nums, int sum, int target). You may assume that this is always called with an initial index of 0, and an initial sum of 0.
Hint: sketch out the alternative paths (a binary tree) on an example input, showing the alternative sums possible at each step. This should help you to determine the recursive steps and base cases.
Submit
Submit your solution:
submit 2030 lab6 RecursiveTasks.javaor if you are working in a group:
submit 2030 lab6 RecursiveTasks.java group.txt