Lab 7: Emulating recursion using a stack

When you run a recursive method on a computer, the method and all of its recursive invocations occupy space in a region of memory named the call stack. Stack memory is special because it can be allocated and deallocated very quickly which is important for efficient method execution. However, this speed is obtained by restricting the total amount of stack memory. If you try to run a recursive method to solve a large problem you can easily exceed the amount of available stack memory which will cause your program to crash. This lab demonstrates how to transform a recursive method into an iterative method my manually emulating the call stack. Students will use this technique to compute Fibonacci numbers, but only a small amount of modification to the source code is required to apply this technique to any recursive problem.

Fibonacci numbers

The sequence of numbers:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

is called the Fibonacci sequence. The Fibonacci sequence can be defined recursively as:

• F(0) = 0
• F(1) = 1
• F(n) = F(n - 1) + F(n - 2) for integer n > 1

In other words, the n^th Fibonacci number is the sum of the previous two Fibonacci numbers.

Consider the following recursive implementation for computing the Fibonacci number F(n):

01  public class Fibonacci {
02    private static Map<Integer, BigInteger> cache = new HashMap<Integer, BigInteger>();
03
04    public static BigInteger fib(int n) {
05      BigInteger sum = null;
06      if (n == 0) {
07        sum = BigInteger.ZERO;
08      }
09      else if (n == 1) {
10        sum = BigInteger.ONE;
11      }
12      else if (Fibonacci.cache.containsKey(n)) {
13        sum = cache.get(n); 
14      }
15      else {
16        BigInteger fMinus1 = Fibonacci.fib(n - 1);
17        BigInteger fMinus2 = Fibonacci.fib(n - 2);
18        sum = fMinus1.add(fMinus2);
19        Fibonacci.cache.put(n, sum);
20      }
21      return sum;
22    }
23  }

The implementation above uses a technique called memoization; it stores the value of F(n) in the map named cache so that the value of F(n) can be reused (instead of recursively recomputed) when some larger Fibonacci number is computed. For example, invoking fib(5) causes the values of F(5), F(4), F(3), and F(2) to be stored in cache. If fib(6) is then invoked, the values of F(5) and F(4) can be retrieved from the cache to efficiently compute the value of F(6). It is possible to show that the method above has complexity O(n) in contrast to the naive implementation that does not use memoization which has complexity O(2ⁿ).

One problem with the above implementation, and with recursive implementations in general, is that there is a limit to the amount of memory that can be used to store the active method invocations, and this limit is much smaller than the total amount of memory available. For example, on my computer I can successfully invoke fib(5411), but invoking fib(5412) causes a StackOverflowError exception to be thrown. 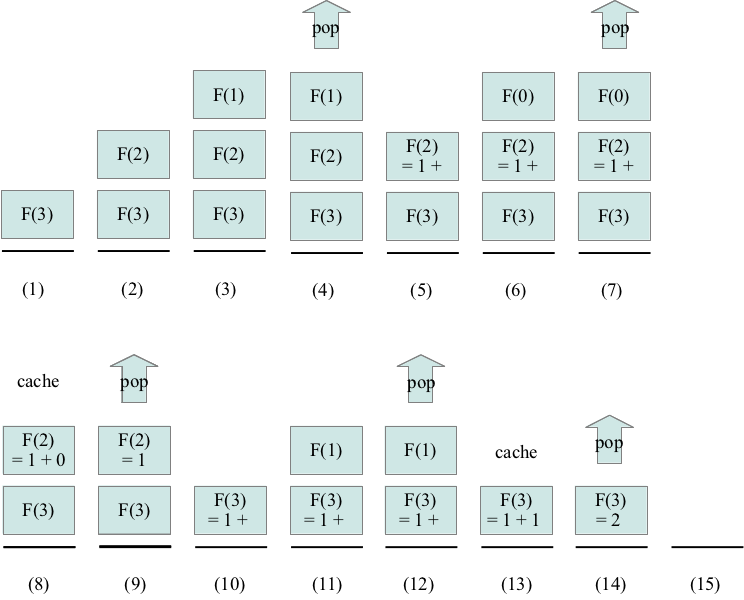To understand why a StackOverflowError exception is thrown, consider the following illustration of what occurs when fib(3) is invoked:

1. An invocation of fib begins execution to compute F(3). A block of memory called a frame that contains storage for the method parameters, references to static variables, local variables, and the return value is allocated from a part of memory called the stack. Because the frame is allocated from the stack, the frame is often called a stack frame.
2. To compute F(3), an invocation of fib begins execution to compute F(2). Another block of memory is allocated for the stack frame for F(2).
3. To compute F(2), an invocation of fib begins execution to compute F(1). Another block of memory is allocated for the stack frame for F(1).
4. F(1) is a base case so the value of 1 can be returned to the calling method F(2) and the memory associated with the stack frame can be freed from use (or popped from the top of the stack).
5. The method invocation that is computing F(2) (whose frame is now on the top of the stack) receives the return value of F(1), and can resume execution.
6. To continue computing F(2), an invocation of fib begins execution to compute F(0). Another block of memory is allocated for the stack frame for F(0).
7. F(0) is a base case so the value of 0 can be returned to the calling method F(2) and the memory associated with the stack frame can be freed from use (or popped from the top of the stack).
8. The method invocation that is computing F(2) (whose frame is now on the top of the stack) receives the return value of F(0), and can resume execution. It computes the sum F(1) + F(0) and caches the result.
9. The method invocation that is computing F(2) is finished execution so the value of 1 can be returned to the calling method F(3) and the memory associated with the stack frame can be freed from use (or popped from the top of the stack).
10. The method invocation that is computing F(3) (whose frame is now on the top of the stack) receives the return value of F(2), and can resume execution.
11. To continue computing F(3), an invocation of fib begins execution to compute F(1). Another block of memory is allocated for the stack frame for F(1).
12. F(1) is a base case so the value of 1 can be returned to the calling method F(3) and the memory associated with the stack frame can be freed from use (or popped from the top of the stack).
13. The method invocation that is computing F(3) (whose frame is now on the top of the stack) receives the return value of F(1), and can resume execution. It computes the sum F(2) + F(1) and caches the result.
14. The method invocation that is computing F(3) is finished execution so the value of 2 can be returned to the calling method and the memory associated with the stack frame can be freed from use (or popped from the top of the stack).

Notice that in the picture above, the stack of frames grows because the bottom-most frame (which is trying to compute F(3)) must wait for all of the frames above it to finish executing (to compute F(2) and then F(1)) before it can finish executing. This can become problematic because each stack frame requires enough memory to store:

• the value of the parameter n
• a reference to cache
• the value of the return value result
• the value of the local variable fMinus1 (used to store F(n - 1))
• the value of the local variable fMinus2 (used to store F(n - 2))
• possibly some other book keeping values such as where the return value should be copied to and the address of where the next stack frame is located

When we try to invoke fib(5412) we end up with a stack of 5412 frames, each requiring memory as described above. This turns out to exceed the available stack space on my JVM. Stack memory is special because it can be allocated and deallocated very quickly; this is important for efficient method execution. However, this speed is obtained by restricting the amount of stack memory.

A larger pool of memory called the heap is available to your program. Heap memory is used to store objects (i.e., heap memory is allocated whenever the new operator is used). Allocating and deallocating heap memory is slower than for stack memory, but the size of the heap is much larger. If we can convert our recursive implementation into an iterative implementation where we replace stack frames with objects, then we might be able to compute values such as fib(5412) and larger. To do so, we have to mimic how the JVM implements its call stack by creating and managing our own stack of frames.

Implement the class FibonacciStackFrame:

• Add the classes FibonacciStackFrame and Fibonacci to the package eecs2030.lab7.
• The API for FibonacciStackFrame can be found here. Note that the API is unusual in that it describes many implementation details (which are not normally part of an API) to help you complete the implementation.
• A FibonacciStackFrame has the following fields:
  • a static field named cache that corresponds to the cache in the recursive implementation
  • a field named n that stores which Fibonacci number is being computed (the n in F(n)).
  • a field named caller that is a reference to the stack frame that created this stack frame; this field is required so that this stack frame knows where to return the value of F(n)
  • a field named fMinus1 that stores the value of F(n - 1) returned by another stack frame instance; this field corresponds to the variable named fMinus1 in the recursive implementation
  • a field named fMinus2 that stores the value of F(n - 2) returned by another stack frame instance; this field corresponds to the variable named fMinus2 in the recursive implementation
  • a field named sum that stores the value of F(n - 1) + F(n - 2) returned by another stack frame instance; this field corresponds to the variable named sum in the recursive implementation
• The constructor should assign a value to all of the non-static fields. You need to choose an initial value for fMinus1 and fMinus2 that indicates that these values have not been computed yet. You can use null or a negative value.
• The method receiveReturnValue simulates lines 16 and 17 of the recursive method. This method should be called exactly twice by two other FibonacciStackFrame instances (once to set the value of fMinus1 and once to set the value of fMinus2).
• The method returnValueToCaller simulates line 21 of the recursive method. This method should invoke receiveReturnValue on the creator of this stack frame (if the creator is not null) and then pop the call stack.
• The method getReturnValue allows the client that created the initial FibonacciStackFrame instance to retrieve the final value of F(n)
• The method execute simulates lines 6 through 21 of the recursive method. To simulate a recursive invocation, you should create a new FibonacciStackFrame instance and push it onto the call stack.
• Test your stack using the JUnit test FibonacciStackFrameTest.
• Use the method fib2 in the Fibonacci class to compute the value of F(10000) by running the main method in the Fibonacci class.

Submission instructions

Submit your solution using the command:

submit 2030 lab7 FibonacciStackFrame.java

or if you are working in a group:

submit 2030 lab7 FibonacciStackFrame.java group.txt