EECS2030 Lab 6

Introduction

This lab has you implement four recursive algorithms. You should review the course notes and lecture slides before attempting this lab.

For Questions 1–3, you are given examples that should help you determine the base case(s) and the recursive invocation. For Questions 4 and 5, you need to find the base cases and recursive invocations on your own.

Introduction

Please create a class named Recursion inside the package eecs2030.lab6

The API for the Picture class that you will be using in Question 5, and the methods you need to implement for the lab are here:

• lab APIs

The Jar file for Picture is here:

• Jar file

Starter code is here:

• starter code

Question 4 requires digital pictures as input. You can easily load the pictures into your program if you place the picture files in the same directory as the package eecs2030.lab6. Some test pictures for Question 4 are here:

• picture 1
• picture 2
• picture 3

Question 1: Compute the sum of the first n integers

Computing the sum of the first n positive integers can be performed by recursive addition. For example, the sum of the first 6 positive integers could be computed like so:

  6 + 5 + 4 + 3 + 2 + 1 
= 6 + (5 + 4 + 3 + 2 + 1)
= 6 + (5 + (4 + 3 + 2 + 1))
= 6 + (5 + (4 + (3 + 2 + 1)))
= 6 + (5 + (4 + (3 + (2 + 1))))
= 6 + (5 + (4 + (3 + (2 + (1)))))    base case

where the expression inside the red parentheses represents a recursive call. Implement the method sum(int n) that uses recursion to compute the sum of the first n positive integers (1, 2, 3, ..., n).

Question 2: Reverse a string

Creating a new string that is equal to the reversal of another string s can be performed by recursively adding the character at the end of s to the front of the new string, removing the last character from s in the recursive call. For example, the reversal of "banana" could be computed like so:

  reverse("banana")
→ 'a' + reverse("banan")
→ 'a' + 'n' + reverse("bana")
→ 'a' + 'n' + 'a' + reverse("ban")
→ 'a' + 'n' + 'a' + 'n' + reverse("ba")
→ 'a' + 'n' + 'a' + 'n' + 'a' + reverse("b")
→ 'a' + 'n' + 'a' + 'n' + 'a' + 'b' + reverse("")
→ 'a' + 'n' + 'a' + 'n' + 'a' + 'b' + ""            base case

The base case occurs when the string s has length equal to 0.

Implement the method reverse(String s) using the recursive algorithm described above. You cannot actually remove the last character from a string because strings are immutable; for a string s you can obtain the substring containing all the characters of s except the last element by using substring:

String allButLastChar = s.substring(0, s.length() - 1);

Question 3: Find the minimum element in a list

The minimum element of a list can be found recursively by finding the minimum of the first element in the list and the remaining elements of the list (the second element to the end). For example, consider finding the minimum element of the list [34, 98, 5, 32, 73]:

  min([34, 98, 5, 32, 73])
= min(34, min([98, 5, 32, 73]))                  recursive call
= min(34, min(98, min([5, 32, 73])))             recursive call
= min(34, min(98, min(5, min([32, 73]))))        recursive call
= min(34, min(98, min(5, min(32, min([73])))))   base case, return 73
= min(34, min(98, min(5, min(32, 73))))          return 32
= min(34, min(98, min(5, 32)))                   return 5
= min(34, min(98, 5))                            return 5
= min(34, 5)                                     return 5
= 5

Implement the method public static int min(List<Integer> t) by recursively finding the minimum of the first element of the list and the remaining elements of the list. You should not remove the first element from the list; for a list of integers t you can obtain the sublist containing all the elements of t except the first element by using subList:

List<Integer> u = t.subList(1, t.size());

To find the minimum of two integers you can use Math.min.

Question 4: Downsampling a picture by a factor of 2

A digital picture's resolution is determined by the number of pixels used to create the image. A common operation on digital pictures is scaling the size of the image. Increasing the size of the image is called upsampling and decreasing the size of an image is called downsampling.

Optimal up- or downsampling by an arbitrary factor is an interesting topic that is beyond the scope of first-year computing and mathematics. However, downsampling by factors that are a power of 2 can be performed using recursion to achieve good results.

To downsample a picture by a factor of 2, we can average the color of every non-overlapping 2x2 block of pixels. The following image shows how we can downsample a 4x4 picture to produce a new 2x2 picture:

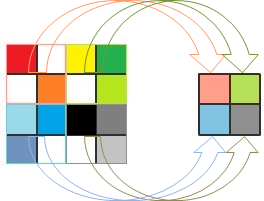
The arrows show that the color of the pixel in the downsampled picture is the average color of four pixels in the original image. Downsampling the 2x2 picture would produce a 1x1 picture (the original 4x4 picture downsampled by a factor of 4).

Implement the method downsample(Picture p, int n) that downsamples p by a factor of 2 n times. A precondition of the method is that the width and height of the picture are both multiples of 2ⁿ.

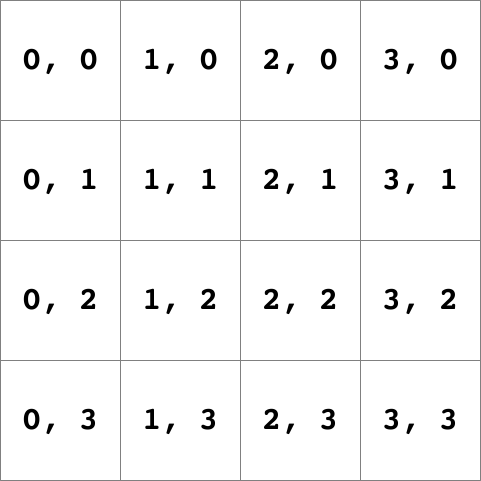
Picture is a class that allows you to load, display, and manipulate the pixels of a digital picture. The pixels are indexed using zero-based integer coordinates (x, y) where (0, 0) is the top-left corner of the picture. Here are the coordinates for a 4x4 picture:

Pixels in a picture are represented using java.awt.Color. A Color has a red, green, and blue integer component. To average four colors, you can do the following:

/* for Color references c1, c2, c3, and c4 */

int r = c1.getRed() + c2.getRed() + c3.getRed() + c4.getRed();
int g = c1.getGreen() + c2.getGreen() + c3.getGreen() + c4.getGreen();
int b = c1.getBlue() + c2.getBlue() + c3.getBlue() + c4.getBlue();

Color avg = new Color(r / 4, g / 4, b / 4);

You can create a new Picture from a file by using the appropriate constructor:

Picture p = new Picture("snowflake.jpg");

Question 5: Binary search

Binary search is a technique that searches for a given element in a sorted list. Binary search recursively examines the middle element of the list to determine which half of the list the target element must lie in. If the searched for element is in the list then binary search should return the index where the element is located. Consider searching for the string "m" in the list ["a", "b", "c", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p", "q", "r"] (notice that the "d" is missing from the list):

  bsearch("m", ["a", "b", "c", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p", "q", "r"])
  
→ there are 17 elements in the list, examine the 9th element and decide which half to recursively search
→ 9 + bsearch("m", ["k", "l", "m", "n", "o", "p", "q", "r"])

→ there are 8 elements in the list, examine the 4th element and decide which half to recursively search
→ 9 + bsearch("m", ["k", "l", "m"])

→ there are 3 elements in the list, examine the 2nd element and decide which half to recursively search
→ 9 + 2 + bsearch("m", ["m"])

→ there is 1 element in the list, if the element in the list is greater than or equal to "m" return 0 otherwise return 1
→ 9 + 2 + 0
→ 11

If the searched for element is not in the list, then binary search should return the index where the element would be if it were inserted into the list. Consider searching for the string "d" in the same list as above:

  bsearch("d", ["a", "b", "c", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p", "q", "r"])
  
→ there are 17 elements in the list, examine the 9th element and decide which half to recursively search
→ bsearch("d", ["a", "b", "c", "e", "f", "g", "h", "i"])

→ there are 8 elements in the list, examine the 4th element and decide which half to recursively search
→ bsearch("d", ["a", "b", "c"])

→ there are 3 elements in the list, examine the 2nd element and decide which half to recursively search
→ 2 + bsearch("d", ["c"])

→ there is 1 element in the list, if the element is greater than or equal to "d" return 0 otherwise return 1
→ 2 + 1
→ 3

Implement the method public static int bsearch(String s, List<String> t) that performs recursive binary search for a string s in an already sorted list t. You should not modify the list t. Use the list method subList to get the half of the list that you need to search for each recursive call.

Submit

Submit your solution:

submit 2030 lab6 Recursion.java

submit 2030 lab6 Recursion.java group.txt