CSE1541 Lab 07

Introduction

This lab has you write small scripts and functions to perform some small simulations; Questions 3 and 4 are especially relevant for students studying experimental physics.

You should put the MATLAB code for your simulations in a single script; the first question also requires you to write a function.

Question 1: The infinite monkey theorem

In Professor Stewart's Hoard of Mathematical Treasures, Ian Stewart writes: "It is said that if a monkey sat at a typewriter and kept hitting keys at random, then eventually it would type the complete works of Shakespeare. This statement dramatises two things about random sequences: anything can turn up, and, therefore, the result need not appear random. The infinite monkey theorem goes further, and states that, if the monkey keeps typing for ever, then the probability that it will eventually type any given text is 1."

To test this theorem, complete the following function:

function [ s ] = randstr(n)
%RANDSTR Random all uppercase string of letters
%  S = RANDSTR(N) returns a random all uppercase string of length
%  N where the characters are English letters.

% NOTE TO STUDENTS: the letters A through Z correspond to the
% integers 65 through 90, respectively. To implement this function,
% all you need to do is generate a row vector of N random integers
% between 65 and 90 inclusive and convert the vector to a string
% using the function 'char'



end

Using your function, write a simulation that runs for 1,000,000 trials. Each trial, use your function to generate a random 3-letter string. Count the total number of times that the string 'ROM' appears (the first three letters of ROMEO) in the 1,000,000 trials, and output the count at the end of all of the trials. Use the MATLAB function strcmp to compare two strings for equality.

The Wikipedia article on the infinite monkey theorem contains some interesting results; in particular, what happened when the theorem was tested using actual monkeys http://en.wikipedia.org/wiki/Infinite_monkey_theorem#Real_monkeys.

Question 2: The birthday problem

A classic problem in introductory statistics is the birthday problem: In a group of N people, what is the probability that at least two people share the same birthday (ignoring the year). Write a simulation to study this problem for values of N = 1, 2, 3, ..., 80.

Your simulation should use the integers 1, 2, ..., 365 to represent the days of the year (ignoring Feb 29 that occurs during leap years). For each value of N, generate 10,000 groups of N random birthdays and count the number of groups that contain duplicated birthdays; store this count in a vector named C having length N. After your simulation is complete, plot (C / 10,000) versus the vector 1:N; you should get a figure similar to the graph on Wikipedia http://en.wikipedia.org/wiki/Birthday_problem

How can you tell if a vector of birthdays contains one or more duplicated birthdays? Look at the help for the MATLAB function unique.

Question 3: Propagation of errors I

Science students are taught that when measuring two independent quantities Δx₁ and Δx₂ that are being added or subtracted, the error in the sum or difference is the square root of the sum of the absolute errors squared:

Is the equation correct? Write a simulation to check the validity of the equation:

generate a vector x1 that has 1,000 elements; each element should be equal to 10 plus normally distributed noise having standard deviation Δx1 = 1.5
generate a vector x2 that has 1,000 elements; each element should be equal to -10 plus normally distributed noise having standard deviation Δx2 = 2
compute the sum y = x1 + x2
plot the histograms of x1, x2, and y on the same figure (use hold on between histograms)
compute and show the value of Δy using the equation above
compute and show the sample standard deviation of y

If you have done everything correctly, the results of Steps 5 and 6 should be similar.

Question 4: Propagation of errors II

Science students are taught that when measuring a scalar quantity Δx₁, the error in a function of the quantity is given by:

Is the equation correct? Consider the following example:

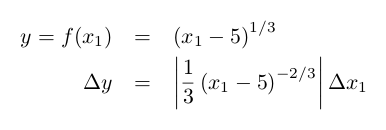
Write a simulation to check the validity of the error equation using the example above:

generate a vector x1 that has 1,000 elements; each element should be equal to 6 plus normally distributed noise having standard deviation Δx1 = 1
compute the function y = (x₁ - 5)^1/3
plot the histogram of x1
in a separate figure, plot the histogram of y
compute and show the value of Δy using the equation above; evaluate the derivative at x1 = 6
compute and show the sample standard deviation of y

If you have done everything correctly, the results of Steps 5 and 6 should be quite different. In a comment, briefly explain why the estimated error Δy from Step 5 is different than the sample standard deviation from Step 6.

Submit

You should have 1 function and 1 script to submit.

Submit your 2 files using the online submit service: https://webapp.eecs.yorku.ca/submit/