CSE1030 Lab 9
Recursive Data Structures
Tue Nov 26 and Thu Dec 5
Due: Mon Dec 9 before 11:59PM
Introduction
This lab has you implement a recursive data structure called a binary search tree. You should review the course notes and lecture slides for linked list before attempting this lab.
This lab is optional. Your lab grade will be computed using the 8 highest grades from the 9 labs.
Binary Search Trees
A binary search tree is a tree where each node has at most two child nodes (usually called the "left" child node and the "right" child node). The left child is the root of the left subtree and the right child is the root of the right subtree. Each node contains a data element, and the nodes of the tree are arranged according to the following 3 rules:
- all of the nodes in the left subtree have data elements that are less than the data element of the root node
- all of the nodes in the right subtree have data elements that are greater than or equal to the data element of the root node
- rules 1 and 2 apply recursively to every subtree
The structure of the binary search tree supports efficient sorting of and searching
for elements in the tree. A variation of the binary search tree called a red-black
tree is used to implement Java's TreeSet and TreeMap data
structures.
An example of a binary search tree of three elements is shown in the figure below:
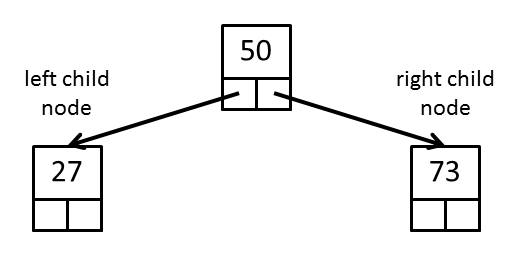
In this tree there is a root node with a data element of 50. The left child node
has a data element of 27 (27 < 50). The right child node has a data element
of 73 (73 ≥ 50).
An example of a binary search tree of eight elements is shown in the figure below:
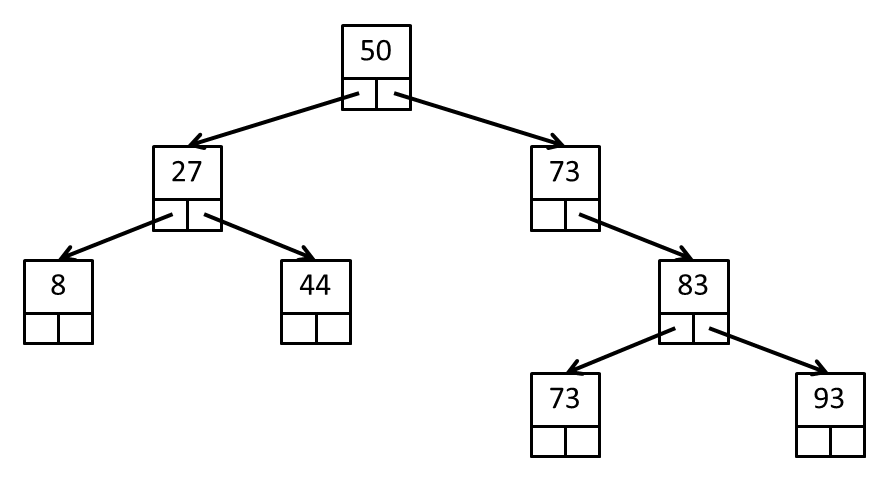
In this tree there is a root node with a data element of 50. The data elements of all
of the nodes in the left subtree of the root are less than 50. The data elements of all
of the nodes in the right subtree of the root are greater than or equal to 50.
If we examine the subtree rooted at the node with data element 27, we see that rules 1 and 2 apply recursively to this subtree: the left child node has a data element of 8 (8 < 27) and the right child node has a data element of 44 (44 ≥ 27).
Similarly, if we examine the subtree rooted at the node with data element 73, we see that rules 1 and 2 apply recursively to this subtree: all of the nodes below the root node of 73 have data values less than or equal to 73.
Adding an element to a binary search tree
The recursive structure of the binary search tree leads to recursive algorithms that
operate on the tree. Consider adding an element to a binary search tree; for example
suppose that we want to add the element 19 to the previous tree:
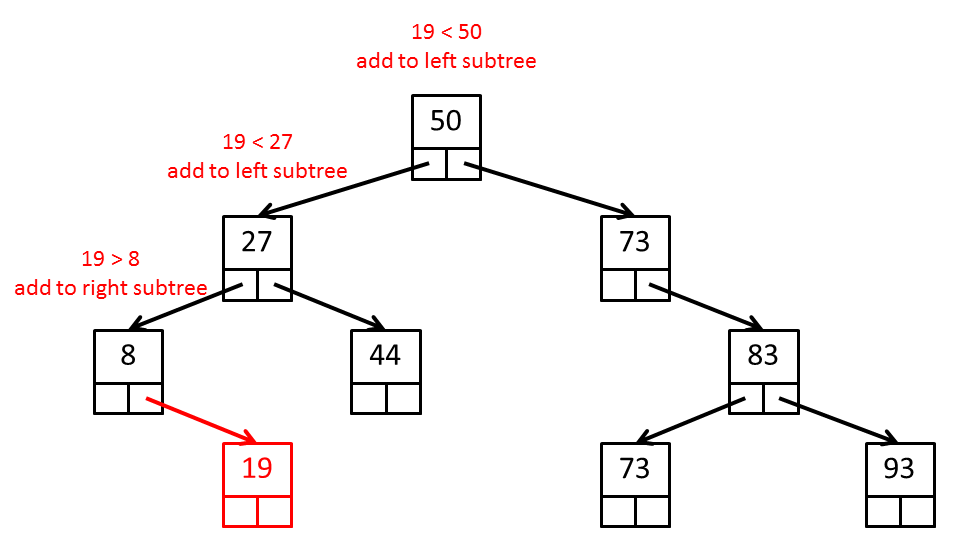
If there is a root node, we compare the element 19 with the data in the root node;
because 19 is less than 50, we know that the element must be added to the left
subtree. We now examine the left subtree that is rooted at the node with data element 27; because 19
is less than 27, we know that the element must be added to the left subtree.
We now examine the left subtree that is rooted at the node with data element 8; because 19
is greater than or equal to 8, we know that the element must be added to the right subtree.
Because the right subtree is empty, we create a new node with data element 19 and set the
right child node to the new node.
Predecessors and successors in a subtree
Deleting a node from a binary search tree requires finding the inorder predecessor
or successor node in a subtree of the node being deleted. Recall that the
inorder predecessor in a subtree rooted at a node N is the node in the subtree
having the data element that immediately precedes the data element of N;
in other words, it is the node having the largest data element in the left subtree of N.
Similarly, the inorder successor of node N is the node having the
smallest data element in the right subtree of N.
Predecessors and successors in a subtree were discussed in the lecture on Tue Nov 26.
Question 1: Complete the implementation of BinarySearchTree
Complete the implementation of BinarySearchTree. The API for all
methods (private and public) can be found here:
Starter code can be found here:
A JUnit tester can be found here:
You need to implement seven methods:
private static <E extends Comparable<? super E>> void add(E element, Node<E> subtreeRoot) private static <E extends Comparable<? super E>> boolean contains(E element, Node<E> subtreeRoot) private static <E> String toString(Node<E> subtreeRoot) public static <E> Node<E> minimumInSubtree(Node<E> subtreeRoot) public static <E> Node<E> maximumInSubtree(Node<E> subtreeRoot) public static <E> Node<E> predecessorInSubtree(Node<E> subtreeRoot) public static <E> Node<E> successorInSubtree(Node<E> subtreeRoot)
A Note on Syntax
You are asked to implement a binary search tree using generics. In other words, we should be able to create a tree that holds elements of any type that has a natural ordering:
BinarySearchTree<Integer> t = new BinarySearchTree<Integer>(); BinarySearchTree<String> u = new BinarySearchTree<String>(); BinarySearchTree<Date> v = new BinarySearchTree<Date>();
The tree
should be able to hold elements of any type that implements the
Comparable interface. In Java, this is expressed as follows:
public class BinarySearchTree<E extends Comparable<? super E>>
E is used as the name of the type of element that the tree
holds. E extends Comparable<? super E> means that
the type E must also implement the Comparable
interface (so that we can perform the less than and greater than or equal
to comparisons using compareTo). The type E does not need to implement
Comparable<E>, however. As long as E
implements Comparable<T> where T is
a super class of E we can still use compareTo
to compare elements. The actual type T is unimportant.
The syntax ? super E is used to
indicate that there is some unnamed type that is a super class of E.
Submit your work
Submit your program using the command:
submit 1030 L9 BinarySearchTree.java