CSE1030 Lab 8

Introduction

This lab has you implement four recursive algorithms. You should review the course notes and lecture slides before attempting this lab.

For Questions 1–3, you are given examples that should help you determine the base case(s) and the recursive invocation. For Question 4, you need to find the base cases and recursive invocations on your own.

Introduction

Please create a class named Recursion inside the package cse1030.img

The API for the Picture class that you will be using in Question 4, and the methods you need to implement for the lab are here:

lab APIs

The Jar file for Picture is here:

Jar file

Starter code is here:

starter code

Question 4 requires digital pictures as input. You can easily load the pictures into your program if you place the picture files in the same directory as your package. Some test pictures for Question 4 are here:

Question 1: Integer Multiplication as Recursion

Computng the product of multiplication can be implemented by recursive addition. For example:

  8 * 4
= 8 + (8 * 3)
= 8 + (8 + (8 * 2))
= 8 + (8 + (8 + (8 * 1)))
= 8 + (8 + (8 + (8 + (8 * 0)))       base case (multiplication by zero)

Implement the method multiply(int m, int n) using recursive addition. Your method should handle the cases where m and n are negative.

Question 2: Search for an element in a list

Searching a list for a particular element can be performed by recursively examining the first element of the list. If the first element is the element we are searching for then we can return true; otherwise, we recursively examine the sub-list starting at the next element. For example, suppose that we are searching for the string "X" in this list ["Z", "Q", "B", "X", "J"]:

  contains(X", ["Z", "Q", "B", "X", "J"])
→ "X".equals("Z") == false
→ contains("X", ["Q", "B", "X", "J"])  recursive call
→ "X".equals("Q") == false
→ contains("X", ["B", "X", "J"])       recursive call
→ "X".equals("B") == false
→ contains("X", ["X", "J"])            recursive call
→ "X".equals("X") == true              done!

The base case occurs when the list is empty.

Implement the method contains(T element, List<T> t) using the recursive algorithm described above. You do not need to actually remove the first element from the list; for a list t of any type T you can obtain the sublist containing all the elements of t except the first element by using subList:

List<T> u = t.subList(1, t.size());

Question 3: Determine if an integer is prime

Sometimes a recursive method needs information that the client should not be responsible for providing. For example, we can determine if an integer x is prime by dividing it by all integers betweeen 2 and sqrt(x) and checking if the remainder after any of the divisions is zero. If we implement this algorithm recursively, then the method needs to know the values of the dividend x and the divisor. The client does not care about the divisor, and should not be responsible for providing the divisor. We can hide the divisor from the client by providing a public method isPrime(int x) that does nothing but invoke the private recursive method isPrime(int x, int divisor):

public boolean isPrime(int x) {
    return isPrime(x, 2);
}

private boolean isPrime(int x, int divisor) {
  // ...
}

For example, consider determining if 17 is prime:

  isPrime(17)
= isPrime(17, 2)      17 % 2 == 1, recursive call
= isPrime(17, 3)      17 % 3 == 2, recursive call
= isPrime(17, 4)      17 % 4 == 1, recursive call
= isPrime(17, 5)      5 > sqrt(17), base case
= true

Also, consider determining if 25 is prime:

  isPrime(25)
= isPrime(25, 2)      25 % 2 == 1, recursive call
= isPrime(25, 3)      25 % 3 == 1, recursive call
= isPrime(25, 4)      25 % 4 == 1, recursive call
= isPrime(25, 5)      25 % 5 == 0, base case
= false

Implement the method isPrime(int x, int divisor) using recursion to divide x by an increasing divisor and checking if the remainder after division is equal to zero.

Question 4: Downsampling a picture by a factor of 2

A digital picture's resolution is determined by the number of pixels used to create the image. A common operation on digital pictures is scaling the size of the image. Increasing the size of the image is called upsampling and decreasing the size of an image is called downsampling.

Optimal up- or downsampling by an arbitrary factor is an interesting topic that is beyond the scope of first-year computing and mathematics. However, downsampling by factors that are a power of 2 can be performed using recursion to achieve good results.

To downsample a picture by a factor of 2, we can average the color of every non-overlapping 2x2 block of pixels. The following image shows how we can downsample a 4x4 picture to produce a new 2x2 picture:

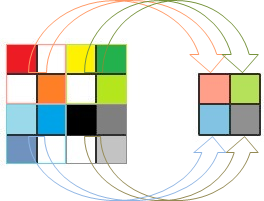
The arrows show that the color of the pixel in the downsampled picture is the average color of four pixels in the original image. Downsampling the 2x2 picture would produce a 1x1 picture (the original 4x4 picture downsampled by a factor of 4).

Implement the method downsample(Picture p, int n) that downsamples p by a factor of 2 n times. A precondition of the method is that the width and height of the picture are both multiples of 2ⁿ.

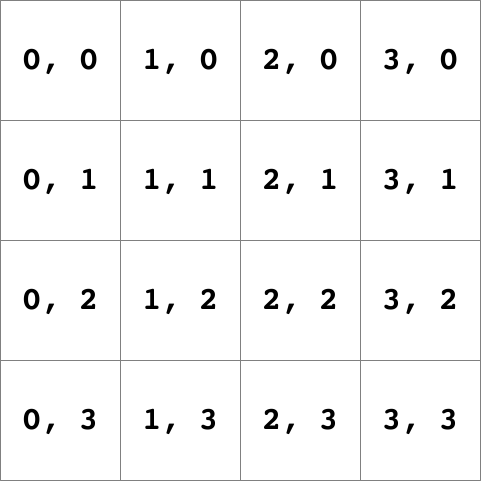
Picture is a class that allows you to load, display, and manipulate the pixels of a digital picture. The pixels are indexed using zero-based integer coordinates (x, y) where (0, 0) is the top-left corner of the picture. Here are the coordinates for a 4x4 picture:

Pixels in a picture are represented using java.awt.Color. A Color has a red, green, and blue integer component. To average four colors, you can do the following:

/* for Color references c1, c2, c3, and c4 */

int r = c1.getRed() + c2.getRed() + c3.getRed() + c4.getRed();
int g = c1.getGreen() + c2.getGreen() + c3.getGreen() + c4.getGreen();
int b = c1.getBlue() + c2.getBlue() + c3.getBlue() + c4.getBlue();

Color avg = new Color(r / 4, g / 4, b / 4);

You can create a new Picture from a file by using the appropriate constructor:

Picture p = new Picture("snowflake.jpg");

Submit

Submit your solution:

submit 1030 L8 Recursion.java