Dragon Curves

The Heighway dragon curve can be defined as follows: Starting with a line segment of length L:

1. turn 45 degrees left or right
2. replace the line segment with two equal length line segments forming a right angle

If you repeat the process with each new line segment, alternating the turning direction for each adjacent line segment, over and over again (an infinite number of times) you get the Heighway dragon curve. The dragon curve is mathematically interesting because it is an infinitely long curve that occupies a finite area. It was one of many known fractal curves.

Here is an example of constructing a dragon curve (by Guillaume Jacquenot).

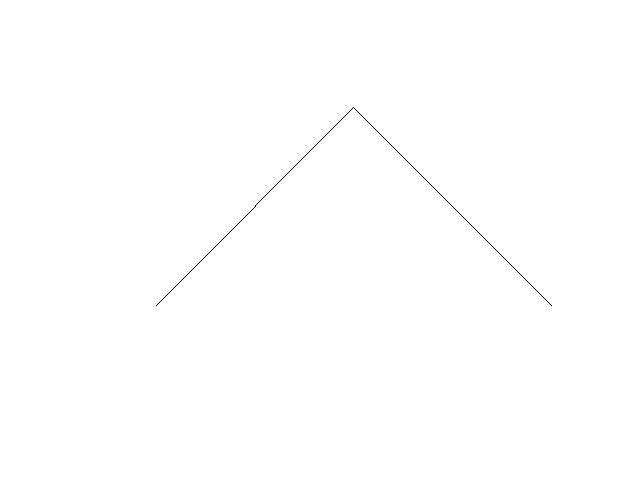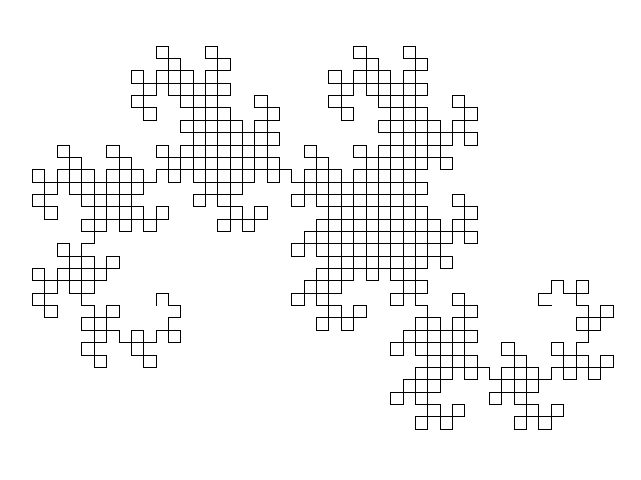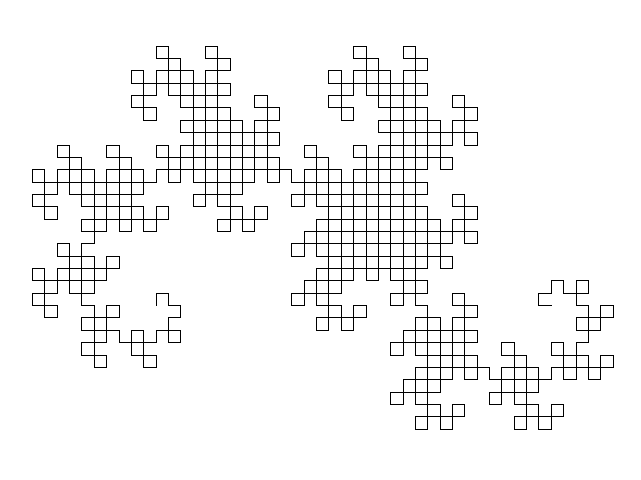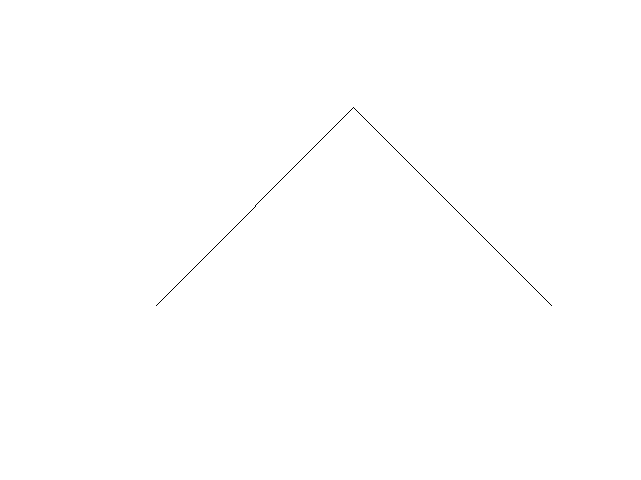
Our turtle can't turn 45 degrees, but we can generate a rotated version of the dragon curve by turning 90 degrees instead:

1. turn the turtle left or right
2. move the turtle forward a distance of L/sqrt(2)
3. turn right or left
4. move the turtle forward a distance of L/sqrt(2) (to finish the right angle)

If everytime the turtle moves forward you repeat the above steps then you will generate the dragon curve. The key to making this work is to encapsulate the above steps in a method, and have the method call itself. Such a method is called a recursive method, and we will be studying these in greater detail later in the course. For now, use the program below to test your Turtle class. You should get the following output:

The main method of the program creates 4 Turtle objects (3 of them using a copy construtor). Each turtle is responsible for drawing one dragon curve. The important methods in this program are the dragon and reverseDragon methods which draw a dragon curve for each turtle they are given. The methods implement the algorithm described above except that every move forward step is replaced with another pair of invocations of dragon and reverseDragon. We cannot do this forever without running out of memory, so an additional method parameter (n) is used to control the number of times we recursively invoke the methods. By decreasing n each time we invoke the methods we eventually reach the case where n == 0 at which point we finally tell the turtle to move forward and draw the line.

package cse1030.drawing;

import java.awt.Color;
import java.util.ArrayList;
import java.util.List;

public class DragonCurve {
  
  private static final double SQRT2 = Math.sqrt(2.);

  private static void dragon(List<Turtle> turtles, double length, int n) {
    if (n == 0) {
      for (Turtle t : turtles) {
        t.move(length);
      }
    } else {
      for (Turtle t : turtles) {
        t.turnRight();
      }
      DragonCurve.dragon(turtles, length / DragonCurve.SQRT2, n - 1);
      for (Turtle t : turtles) {
        t.turnLeft();
      }
      reverseDragon(turtles, length / DragonCurve.SQRT2, n - 1);
      for (Turtle t : turtles) {
        t.turnLeft();
      }
    }
  }

  private static void reverseDragon(List<Turtle> turtles, double length, int n) {
    if (n == 0) {
      for (Turtle t : turtles) {
        t.move(length);
      }
    } else {
      for (Turtle t : turtles) {
        t.turnRight();
      }
      DragonCurve.dragon(turtles, length / DragonCurve.SQRT2, n - 1);
      for (Turtle t : turtles) {
        t.turnRight();
      }
      reverseDragon(turtles, length / DragonCurve.SQRT2, n - 1);
      for (Turtle t : turtles) {
        t.turnLeft();
      }
    }
  }

  public static void main(String[] args) {
    List<Turtle> turtles = new ArrayList<Turtle>();
    turtles.add(new Turtle());
    for (int i = 1; i < 4; i++) {
      Turtle u = new Turtle(turtles.get(i - 1));
      u.turnLeft();
      turtles.add(u);
    }

    turtles.get(1).setPenColor(Color.RED);
    turtles.get(2).setPenColor(Color.BLUE);
    turtles.get(3).setPenColor(Color.GREEN);
    
    DragonCurve.dragon(turtles, 8, 11);
  }
}