CSE1030Z Sample Exam Questions

Random

1. Explain why a static method cannot use the non-static attributes of an object using this.

A static method is associated with a class rather than with object instances of the class; thus, there is no instance for this to refer to.

2. What is a singleton?

A singleton is a class that is instantiated exactly once and is used to ensure that there is at most one instance of the class and to provide a global point of access to the instance.

3. What is the difference between an overloaded method and an overridden method? Can you override an overloaded method?

An overloaded method is a method that has the same name as another method in the same class; the signature of the overloaded methods must be different. An overridden method is a method in a subclass that has the same signature as a non-private method in one of the superclasses.

4. Suppose that you are implementing an immutable class that has a mutable attribute. What must you do to ensure that objects of your class are truly immutable?

You need to follow the recipe for immutability from the slides on Jan 16.

-there must be no mutator methods
-the class must be marked final so that no one can extend it
-all attributes should be private and final
-must be no privacy leaks of mutable attributes (e.g., defensive copies are required)

5. (too hard for a CSE1030 exam) When implementing equals you were told to use the getClass method to check if the two objects being compared had the same class. Discuss the consequences of using getClass in equals when inheritance is involved.

Using getClass breaks substitutability. Suppose that you have a parent class X and a child class Y. If you implement equals in X using getClass then x.equals(y) is always false for any X instance x and Y instance y (because x.getClass() is not equal to y.getClass()).

6. Suppose that you are implementing the group of classes in an inheritance hierarchy, such as the Dog hierarchy that we studied. When could the topmost class (e.g., Dog) be an interface instead of an abstract class?

The topmost class could instead be an interface if it has only methods and no attributes (because an interface is not allowed to have attributes).

7. What is the most important thing to remember when working with static attributes in an inheritance hierarchy?

There is only one copy of a static attribute and it resides in the class where it was defined; each subclass does not get its own independent copy of the static attribute.

8. Describe the steps that are taken when trying to prove that a recursive algorithm is correct.

1. Prove that the base cases are correct.
2. For each recursive case, assume that the recursive invocation is correct, and prove that the case is correct.

9. What is the purpose of an iterator?

An iterator is an object that lets a client traverse all of the elements of a collection.

10. What is the solution to the puzzle on Slide 3 from Feb 25?

You are not allowed to override equals; however, you are allowed to overload it:

// in Enigma class

public boolean equals(Enigma e) {
  return false;
}

11. What is the definition of a binary search tree?

A binary search tree is a binary tree where the nodes are arranged according to three rules:

1. all of the nodes in the left subtree have data elements that are less than the data element of the root node
2. all of the nodes in the right subtree have data elements that are greater than or equal to the data element of the root node
3. rules 1 and 2 apply recursively to every subtree

12. Why are linked lists and trees considered recursive data structures?

A linked list can be thought of as a sequence of nodes where each node is the head of a sublist.

A tree is an arrangement of nodes where each node is the root of a subtree.

Inheritance

1. What kind of relationship between two classes does inheritance model?

Inheritance models the is-a or is-substitutable-for relationship.

2. Suppose that you have three classes X, Y, and Z, where X is the parent class of Y, and Y is the parent class of Z. Explain what happens when a Z object is created.

The Z constructor runs, which causes the Y constructor to run, which causes the X constructor to run. The X subobject constructor finishes, which allows the Y subobject constructor to finish, which allows the Z object constructor to finally finish. In other words, the subobjects of Z are constructed in order from the top of the hierarchy down.

3. Suppose that you have two classes X and Y, where X is the parent class of Y. Suppose that Y overrides a method named foo:

public class Y {

  // @pre. s begins with the character 'a'
  public int foo(String s) {
     // ...
  }

Give a different and acceptable precondition for foo in class X.

Y must not strengthen the precondition of the method in X; thus, the precondition of the method in X must be stronger than the precondition of the method in Y. There are an infinite number of possibilities:

@pre. s begins with the string "ab"

@pre. s begins with the character 'a' and ends with 'y'

@pre. s begins with the character 'a' and s has length 5

4. Suppose that you have two classes X and Y, where X is the parent class of Y. Suppose that Y overrides a method named bar:

public class Y {

  // @return a list of words that start with the string s
  public List<String> bar(String s) {
     // ...
  }

Give a different and acceptable postcondition for bar in class X.

Y must not weaken the postcondition of the method in X; thus, the postcondition of the method in X must be weaker than the postcondition of the method in Y. There are an infinite number of possibilities:

@return a list of words that contains the string s

@return a list of words that starts with the first character of s

5. Suppose that you have two classes X and Y, where X is the parent class of Y. Suppose that Y overrides a method named baz:

public class Y {

  public void baz() throws Exception {
     // ...
  }

Give all of the possible legal signatures plus throw clauses for baz in class X that throw only a single kind of throwable object (ignoring overloaded versions of baz).

The method in Y must only throw exceptions that are substitutable for the exceptions thrown by the methods in X. In other words, the method in X can throw an instance of any superclass of Exception. In Java, Throwable is the root class of all throwable objects, so there are only two possible solutions:

baz() throws Exception

baz() throws Throwable

GUIs

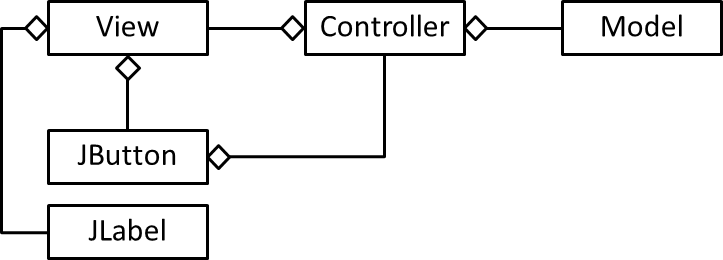
1. Draw the UML class diagram for the dice rolling GUI application from the Mar 04 lecture:

Your diagram should include the model, view, controller, JLabel, and JButton classes, plus any other classes that you think are necessary (do not show any classes related to the image of the die or any inheritance relationships, however).

Recursion

1. What is the maximum number of elements that can be held in a binary search tree of height m? (the height of a tree is the number of levels of the tree.) Such a tree is called a full tree.

m = 1, elements = 1
m = 2, elements = 1 + 2 = 3
m = 3, elements = 1 + 2 + 4 = 7
m = 4, elements = 1 + 2 + 4 + 8 = 15
m = 5, elements = 1 + 2 + 4 + 8 + 16 = 31
m, elements = 2^m - 1

2. Suppose that you have a full tree. What is an approximate recurrence relation for recursive search of the tree? (see question 4 below if you cannot recall the search algorithm) You can assume that checking the base cases and performing a comparison can be done in one unit of time (or constant time).

T(n) is the amount of time that it takes to search a tree having n elements. To search a binary search tree for a particular element, you check if the root node holds the element (this is the base case); if it does not then you perform a comparison to determine which subtree to recursively search. The question says that checking the base cases and performing a comparison can be done in one unit of time. The recursive search must search a tree having approximately n/2 elements. The overall recurrence relation is:

T(n) = T(n / 2) + 1

3. Solve the recurrence relation from the previous question.

T(n) = T(n / 2) + 1
= (T(n / 2 / 2) + 1) + 1
= T(n / 4) + 2
= (T(n / 4 / 2) + 1) + 2
= T(n / 8) + 3
= (T(n / 8 / 2) + 1) + 3
= T(n / 16) + 4
= T(n / 2^k) + k

Solving for k in terms of n by using T(1) = 1 yields

k = log(n)

Substituting k into the recurrence relation yields

T(n) = log(n) ∈ O(log(n))

4. The recursive search algorithm for a binary search tree can be stated as follows (the generic type syntax has been removed for simplicity):

  boolean contains(E element, Node subtreeRoot) {
    if (subtreeRoot == null) {
      return false;
    }
    if (element.equals(subtreeRoot.data)) {
      return true;
    }
    boolean result;
    if (element.compareTo(subtreeRoot.data) < 0) {
      result = contains(element, subtreeRoot.left);
    } else {
      result = contains(element, subtreeRoot.right);
    }
    return result;
  }

(a) Prove that the algorithm terminates.

(b) Prove that the algorithm is correct.

To prove termination:
1. contains(e, node) searches a tree of size n
2. Each recursive call contains(e, node.left) or contains(e, node.right) searches a tree of size n/2 < n for all n > 1

To prove correctness:
1. (Correctness of first base case) If subtreeRoot is null then the element is not in the tree; the base case correctly returns false.
(Correctness of second base case) If the subtreeRoot holds the element then the element is in the tree; the base case correctly returns true.
2. Assume that contains(e, subtreeRoot.left) correctly determines if the left subtree contains e. Assume that contains(e, subtreeRoot.right) correctly determines if the right subtree contains e. If e is smaller than the element in subtreeRoot then it must be in the left subtree; this recursive case invokes contains(e, subtreeRoot.left) which we have assumed correctly searches the left subtree. If e is greater than or equal to the element in subtreeRoot then it must be in the right subtree; this recursive case invokes contains(e, subtreeRoot.right) which we have assumed correctly searches the right subtree.

Data Structures

1. Consider the simple linked list implementation that we studied in this course and Java's ArrayList (which you can think of as being an array that can grow in size): Which is more efficient in terms of big-O complexity for the following operations:

getting an element using an integer index
inserting an element at the front of the list
inserting an element at the back of the list
inserting an element in the middle of the list

Getting an element using an integer index is faster for ArrayList: O(1) vs O(n)

Inserting an element at the front of the list is faster for LinkedList: O(1) vs O(n)

Inserting an element at the back of the list is faster for ArrayList: O(1) vs O(n) unless the LinkedList implementation has a reference to the last element in which case the complexity is the same for both lists.

Inserting an element in the middle of the list is O(1) for a linked list if you are doing a traversal and are at the location where you want to insert; however, the traversal to find the insertion point is O(n), which is the same complexity for inserting into the middle of an ArrayList.

2. Describe an algorithm (recursive or otherwise) that searches a linked list for a given value (returns true if the element is in the list, and false otherwise). Your algorithm can use plain English (instead of a programming language).

An iterative algorithm would look something like:

contains(e):
n = head node
while n is not null {
  if n.data equals e {
    return true
  }
  n = n.next
}
return false

An recursive algorithm would look something like:

contains(e, node):
if node is null {
  return false
}
if node.data equals e {
  return true
}
contains(e, node.next)

3. (too hard for a CSE1030 exam) Describe an algorithm for removing an element from a binary search tree. Your algorithm does not need to be efficient but it must preserve the search tree property of the tree.

You can google the answer for a full explanation; it looks something like this:

if the element is in a leaf node {
  remove the node (set it to null)
}
else if the element is in a node with only 1 child node {
  replace the node with the child node
}
else if the element is in a node with 2 child nodes {
  set the element in the node equal to the largest value in the left subtree of the node
  remove the node containing the largest value in the left subtree of the node
}

4. Draw a binary search tree containing 8 unique integers; the root of your tree must have a left and right child. What is the inorder, preorder, and postorder traversals of the tree you have drawn?

Here is one possibility:

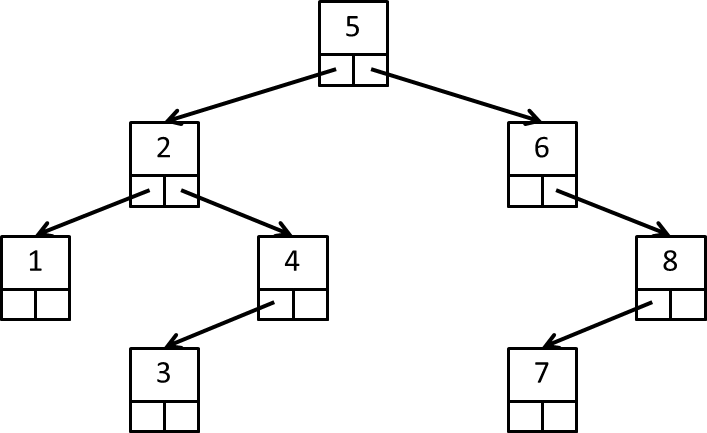
inorder: 1, 2, 3, 4, 5, 6, 7, 8
preorder: 5, 2, 1, 4, 3, 6, 8, 7
postorder: 1, 3, 4, 2, 7, 8, 6, 5

5. Explain how to use a stack to check if a sequence of parentheses is correct nested; you only need to consider round brackets ().

This is a simplified version of eCheck11B from the Apr 1 slides: Process the sequence one character at a time. If the character is an "(" then push it on to the stack. If the character is an ")" then pop the stack. If you ever attempt to pop an empty stack, then there are more closing brackets ")" than opening brackets "(" so the sequence is not correctly nested. If the stack is not empty when you have finished processing the sequence, then there are more opening brackets "(" than closing brackets ")" so the sequence is not correctly nested.

6. (From Introduction to Programming in Java, Sedgewick and Wayne) Suppose that a client performs an intermixed sequence of enqueue and dequeue operations on a queue. The enqueue operations put the integers 0 through 9 in order on the queue; the dequeue operations print out the returned value. Which of the following sequence(s) could not occur?

a. 0 1 2 3 4 5 6 7 8 9
b. 4 6 8 7 5 3 2 9 0 1
c. 2 5 6 7 4 8 9 3 1 0
d. 4 3 2 1 0 5 6 7 8 9

The question says that the numbers are enqueued in order, so the 0 must be the first number enqueued. Because a queue is a first-in-first-out data structure, the first element dequeued must also be the 0. Only one of the sequences (a) starts with 0 so (b), (c), and (d) could not occur.

7. See previous question: Which sequence(s) could have been produced using a stack instead of a queue, and what order of commands must have been given to produce the output? (for the stack, the pop operations print out the returned value)

The easiest way to solve this problem is to draw a stack and check if you can generate the sequences. I will give you the operations that generate as much of the sequences as possible:

a. push(0), pop(), push(1), pop(), push(2), pop(), ..., push(9), pop(), success!

b. push(0), push(1), push(2), push(3), push(4), pop(), push(5), push(6), pop(), push(7), push(8), pop(), pop(), pop(), pop(), pop(), push(9), pop(), fail!

c. push(0), push(1), push(2), pop(), push(3), push(4), push(5), pop(), push(6), pop(), push(7), pop(), pop(), push(8), pop(), push(9), pop(), pop(), pop(), pop(), success!

d. push(0), push(1), push(2), push(3), push(4), pop(), pop(), pop(), pop(), pop(), push(5), pop(), push(6), pop(), push(7), pop(), push(8), pop(), push(9), pop(), success!

CSE1030Z Sample Exam Question Solutions

Random

Inheritance

GUIs

Recursion

Data Structures